{
"$schema": "https://vega.github.io/schema/vega/v5.json",
"usermeta": {
"deneb": {
"build": "1.4.0.0",
"metaVersion": 1,
"provider": "vega",
"providerVersion": "5.22.1"
},
"interactivity": {
"tooltip": true,
"contextMenu": true,
"selection": false,
"highlight": false,
"dataPointLimit": 50
},
"information": {
"name": "Radial Tree with Bars",
"description": "[No Description Provided]",
"author": "Kerry Kolosko",
"uuid": "cd054daf-7d5f-4602-bbd3-f9f2157af70e",
"generated": "2022-11-23T13:49:06.828Z",
"previewImageBase64PNG": "data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAJYAAAByCAYAAACx1Ch2AAAAAXNSR0IArs4c6QAAIABJREFUeF7tfQd8ldX5/3n3nbnZm52BTIGwRJEEEpYodaJCq9Yuq/6t/jqk/hS1Yq2/qtVaR7W2WkoFV5UhARKGICNMWSHMsLKTmzvf/f98r++b3oSbBRiCcj6ffEi4733f95zzPc/zfcZ5DkUut8sj8A2MAPUN3PO7cssEQkgcIeTAd6XDnennZWB1ZrSaXwtQxRJCys79Ft/eb14G1rnPbSohBD8l536Lb+83LwPr3Oe2HyGEIYQcPPdbfHu/eRlY5z63vQghOiGk/Nxv8e395mVgnfvcDieEeC9LrMgDeBlYzcfFQghRjJ/2INeTEFJLCPERQjCODuN3rb0vfhc+vwys5rN8BSGkygBMe/MPYNUQQvyEEAAyjRByxFCP7X33Qn6eQgiJIYTsu5A3Pd97fdeA1Z5kgXqrJISc6sDAXksI2UEIaSSEWAkhmOCjXQwsGyEky3B5QHJ2m/ZdAxasuKuNiTgdYRZg6YmEkJOEEI4QMpAQspcQIodfu3TRluSZd47rLcvyLkJIgBACIh9FCPnKsBQBUDhOPYQQ1lCVze5xARDAE0KuIoRsNt7hAtzywt3iuwAsTCxUBdQWrDiAAFKmPsIwgiclEUIOG5/lGmDBd5taceGBHJ3QW4mu5uRNvmKbITXwOVwPmPBhhJCdBkjxvERCyNYLN22hO8Ub9+1WKtDs43cBWOhrtqHeYMUhFJNMCNkTQW1B6vQ2pJRKCBlrAAvfa2qrV5ROpShqmUpJvfLzB8HdMMr4DtSRYBB5EHu0oYYENP+GNDtBCKk+D6ChD1gA8PpDwna79m0CFiYUFh0A0bINJoTUGeDCdf0NVdVyUkzOAmmDBt4EyRYMv2HR56XfJzT1j5qGGtutt16Fe1xjeOABrAHGtfsNUp9HCFllAABgADf7j/E3AAnpaIKuIwCBoYBnAFRQtd2yfVuABbBA0kB6gPO0bFBPUB0g5gBehvH3phYX0sbEA1gA1BDjO/heUysqLHuY6Pq8vMlZkHDgbZAgsCbhasgxJt1NCHERQvoYahHX9TCugyWJZ+H+JodDHyDdwNMi9QHPxz0ATFxzPhLvGwfjpQwsTAwmAxIDExptqDjwnJa+JEzISELIbsM9AM4FdwHId8s2yZg4gAlq64zx03Rd8cqyZ3VdvzWvIAtk30kI6WuoVvC5fELIBgOYgwwpCiJvN4wBWJIg8pA6AHmpcWOoXahcgMZsZv/IsmVlgrvhzBO33zH+BYMvfuPgOJ8HXMrAwqBD8gBImCgA7Urj72acyBggSDRcA18T1AnUIYiv1GIAARJIDAAK34G6aaaqigrL3iJEH5RXkDWGEJJucCqAB5IL6hMANlUWJBLAj8/wfAAW7glIKwSwAS5YoJBsh4xFgXnBT9MCKVpxcAGhyA2UTo/JnZwBftit26UILKg1EwywtgAumNyYIEwewIAJgwUY3kwwQSKY6hCcCAAKb0iFwf0BTtwbkwswhqnCg//RdUJPnJw146f3/s+E19/6PwACLgpIQdwbfjCTYJsgmEYI2WJIG3yG55jSCm4DuD+OGeAbbYBxOx5aVFg2lxD9GUrXZ+VOzn6/WyPKeLlLDVhQO+Ah4ECYeEgAWHgAzXEDBJBaILaRpBY+g+sAIMC9AD6AqwmEn3++L0VgmH65+dlfGOoLAMD1TdcUrzy4UdfJgbyCrHuKCg+W6UT/z8SC7LmGGgQYTGkH9wWAFQ4kSFqoPYAf7wiDASoTbguAEuoV6Th4vr5qRelMmqI+JoR6Kq8g84lLAVR4x0sNWHhnWFbgU1CBmGyoEag1SA2oMJMEm1wmfC5wLRL0QHxDDsZ3314pfv+H+ZjEUCteUXqbTlPPWFTrqAbtK19ycnLc8OHDmzlTi1cdeInotB6Qqd9YOG23TvSXaFZYrgRFqMi/5E+9YpkBFliGAC6AA98ZjAsAFXwLLge8D8g+1CU+x9/gdVgYdWsLD2equrqZ0KQoLz/r5ksFVJcKsAAAqCSoF1haWAxY1VBRkFJY5bC2IIGgWsxVDysQKjK8mSQeE1dbXHiwXCfk73kFWY+HX1RSUtIvJyfncHFxMRsTE5N05ZVXNgvx7N69O0aSJCYnJ6dmy5YtPWJiYqqOH1KzWU6frhDhbzZbReNVV10Vsuz+89HWWTfcOBKLACDD/00nhJhSDe8IkKEfaOESlRQVHlwP61WlGsfk5+eg7zAO0O9uH+i+VCQWCDUmAVac6XuCFIDZbvKfTGPioLZMMMJHdJYDcfv27QnDhw+vXldUOtER7duN38OBtWvXrvTS0tIzt9xyi7579+7UoUOH4p5Nbe/evXwgEOhx5MiRYxkZGbEsyyqDBw92b9u2rQ8AWVJS4qJpmsd9DbVZl1eQdZ3BwUDcsQAA8gmGtKowIgLghwCTVlR48HVCyE9omrpqwqTMLw11b7oaIoWjupVAu1SAhUGDCkN4BOCCVIKPCJYVuAkABjWCvzFp4C4g0lCLAFfTCi8rKxMaGxt7jBgx4pCu6/TWrVvTRo0aBbXU1DZs2JCo63rg6quv9m7ZsiW95ee4cPPmzXEOh4OrqqpqiI2NTRkyZMixrVu3piuKUsPzPC+KojBu3LgqSLSAN2bYtXmZnxrSNmTtXX/97OmffvrPNYaqxEIYYUgycc3KQw9ouvayTvQfTSzIfsv4HrgYvhuJO3YrUF0qqtAcNAwqVB74FdQKXAz4HdF9mPfwjoMkw2kJMEEiwPQHkW7mjd+0aRN4WmDMmDGNUHsul+tkZmZmk2SDxBEEwTJ48OCqTZs2pY0ZM6aZxDJfqKSkJIXjOFWWZU0QBEYURbyDLS4urr66ujoBgPzyyy97B4PBk06nk1cUJRb3Kl5Z9pCu6y+qFDU2Pz8TMURwRDhYq4sKSycSQq0iFPViXn7mw8azYCUiqoBFdEm0S0limQOKSQCozEAx1AesLxBgkHlYiKEQzN69ex1ut9t11VVXNeNIu3btsvv9/oSxY8ce2759e6rNZvP079+/KTyyceNGK8dxKUePHj2ekZGR1JK8my8yb948+rrrrksSRVHleT6GoqhaRVEsLMviXpCoNQCTpmm1VqtVUFWVBS9bX3xgiixTN+cVZN+77LPdCxYvfnvhO+/+aXnx0r0JGsdtpkjI4pxsSFz0DwtknSF5IYUh3eA3Q5iqW7ZLEViQUiC54FawsuBygNqD4zFEmHfv3t1XkqSKnJwc//bt23sFg8Eqk0y3kDaNPp9PcLlcZODAgc0maefOnWmaprGapvkAhrZmD5JL07SQhSoIgijLMgwJmeM4zefz+WmaDv0/gDVixIg6k4sVryqbDclFCP1IXn7Gu6sLS5dRhBpCKdSY3GmZkJJIHoQVGe6Nh0MWiwdWsNkwBlCV3UZNdkdg4Z3ApUBQW3rFzYHEIELtgVsBEJhUqL5QztMXX3zhpGk6CpIq3IILBwek2caNG3s8++yzjrfffvtEbm4uCHRTg1RTVbWXpmmncnJCFlmbbcuWLcm6rkdpmiZRFMWxLCvSNK14vV7ZZrNFuVyuarfbHe3xeKpiY2PjYRDs2rUrsaFBc1177bCy4hUHn9cp8j86oSZPLMgsNEAF6QxJhX5BUsE1AQ5pAh1jhQA7OFq32obWXYFlcilkZLYWwcdAQ3KBe8BhqoIveTye47m5ucrGjRvTrFarT1VVH03TqcOHDzdN+iaAvPPOO8mffPLJyIceemhrS2DhoptvvvnuQCCwaenSpeB07TYARVGUOFmWFY7jWEVRgizLMpqmaTzPS3tPebPKqxTFwrMJtW61om8K72It7I6JQ1LdZfsb56oKVZs3OftFw1CBIxgxR3A/SCSk/kAimYYG5g6WMVq4RGv3Pbvigu4CLIh7eNDDk9bM3ChwqdbSbpmFC9b+PikxWcjLz34QpFuW5RhwJ13XmR07dqQfOnToTJ8+fdK9Xm85ANdyUO+6665pWVlZtXPnzm3p8yJ33HHHnWlpaVuef/75Du92hoQMBAIJqqrSNpuN2XbY2+9IbTCjutbfKyAqRNKISBPVElT0RivPOmRF88Y5LYGUWMuhyYOHLQ946+aKwaAy5brBz4b1G64WjIfpWsFYwZeHRWcaMl2Blw4/o7sAy7TgMIAQ9WbaiElUIblaxvRCnSwuLH2EE7Sj8UnUShBwuAF0XbfC+oL153Q6ZU3T7BaLpSrc8jNHaPbs2dm1tbVTly9f/kpL6/Guu+6aERsbW/7CCy9EyoJodZAPHDjgLD3VOGzrQfc1VQ3+vgFRljRCyRTRWVnVQ9anJGsix9K8L6h4o2xstE8iDU4Lo08Z0tOf7nJZcydmzjO4FOKIABTiiJgvM78e/NJMdzZjplCHrdGHDoPiQlzYXYBl9sXM7gQRh/mNBtAhxQR8CgA7y+t89OhRS319fZIgCB6QcDhAQaRhzYG8g+ucPn26Ztq0aZGyLZn33nsvLz09HeqwIXxQZ82aNZFhGLJgwYLVHR1s+MYe/9sXg8tP1d4oq0osS1OcruvggLROKIWhCSspmiirRAz9LmsiTREmIGs+h4WNohhajnfZdtwypN+whoaGmJk3j/p1WBo1iDviiJDsJlFHChAMGnDNdrlgR/txvtddbGBBBYKIh/uJACSQd6xMWD4Ag5kkBycoVu5ZGxN0XWe3bduWoCgKw7JsHU3TdkmSIPGsXq+Xs9lsFVdddVVE8/yhhx4ax3Ecef7558FpmtqffvXcRKvgyv7x0z/9S0cGWtd16sm/bhy6/2TlzR6/qFAURdkFxmnlaYRtaIamGIqidElWJVUnkqrpMCY1SdGDABlN07RfVHwCRwlXZ6fqw9OStdz8rMdWLdt326RpAwAmjAmkEhYXeBcWHMAGR2uzLNeOvO83ec3FBpaZ+YlVZybhhUsvAAzEHNwI7wrvO1YsMgYixss2bdoURdM0QipQp7aXX355VEJCgjZ79uyiYcOGNZNI5oPuuuuuTJc9Zvbk6fnzw6XamvmfjRXZYE7BL29+laKoduNzLy0q6bll/4kfNHiCWAhNzSaw9igrHc/SNK8TokqKFgCgoB4VRdUCkup3WDl7g0+u51mat3C0XVSIt2eSc/v3BvUZoqrk8S1b193x6GM/WmyMBfx2CAdBsiPuaDqAwcOQI4b/a9NF8k2CCve+2MAy+2dmYQJAWJlmigrMaGwiReTfTIshW7du7SuKYvXVV1/das63GbrZsmVL0p49e6bl5OR8cvfdd0fcKfOPP/8jLiiq82wW68I5P799o/lS77zzjqWysrLfb37zGxDkNoGl6zr/4+eW/OBUjRe+p7OahaOtsQ4umaEpzgCUqmokGJQ1PySdouoyoSgd13mDilfVdCXaztlvyunnixFsVF5Btpkyg7gpyDv6Ei654UiFSoSUv+j+rO4CLBPkABH4EdQdzGpMJlZ/3IsvvscMHTh6Tl5B1h+Ki4stTqczjeO4iqFDh7a5URPX7t+/P9ftdl/5wgsvvFJdXR1x0Be8syBz9frVtr/97W+QnCFgDxkyxB4TEzNt7dq12PzQJil+9M9Fo/efqr5OkrVImzlCQHNYWEeMnUumaIqGvJJUHVJV8waURk0nqsDRgiegeMDJ7BbOhn+jbNaTf310+muGxERoB1Ieufrm1n4ACioR4A9PSMS4YcHiGV2+k6c7ASt8lZs5V02bI0J55kQbaY9quG306NG1JSUlNlVVkxiGOZmTk9PeZlBq/vz5P9UoTZ+SP+XtSNdPnz49xu/3jy8uLkaw2JSYwtSpUwtGjx69fN68eWe5KswX1nWdu/e5ZfecqWlE6KXN5rSyrsQorh9NUXRQ1htkVZMUVQ8qmi5Lih4CL8dQXFDWAqKsihaO5a4ZEL0yb0ji8aFDh2I8TOBCmiPoDmsZKjH8/ZBeA2cqxgUGT5eHfroTsEBGMaHmpILY46eieMXBCbmTs5asXl2aFhPj0xVF0ex2e53b7XawLMuPGjWqmdc80sy+teit2EMNhz50pjo/mjt9LiRAS6BYxo4dO7WgoGD1k08+CdUbahMmTLjO4XDsWLJkSavb7t9dsSvxs/WHH/QFxVbBF/5OcQ4uKdHFZxFCaSfKj3tOlO22p2WPOklZohpomqKDkuYnRKcBMJ5juL4p0buf/snEdymKkpd/9tX3ps4YDIcoQAwpFc6lIM3gnsB7QFVeNELfnYCFfCoMFjI/Te6E93MWLt+/UeDod66dlP1HTBB8VRaLxerz+WopikqqqampmjFjBtwRrTY4TJ/69KnZDtZBebZ63p03b95ZnGnUqFFjBw4cKL7zzjuhXHO08ePHF6Slpe1auHBhsy1g4Q/631fXjNx1onKGomjtEnx8j6Fp+oo0+7WNdaej3Y3eWt6ZXMHwlqCi6hLUn6TqQVUjiqyoiqIRKdYp1D8158rXj5UFf6Bq5PXlny+a9seXnkDYx5ResJax+xocC7lbLbknYotQhy33AbQnYM/58+4ELHQCrgeELpAZYOaEkzWFpXNs0e6VLMsK1dXVNZMnT/bB+kNGAaQXLMD2AsXmCMFpqmmaHMn1cMMNN/QQBCFj0aJFxeb13/ve96YkJCRUvfnmm01gaznav3y1eMreoxWwxjrcBiUq91WePk4l9h50SNHoBk9AqdIJpQUlxY9/ATBNp2RF1dRoO88+PDPzbY/HU+P3xE3Py8/8m/EguB8wXmbJAFi94eDBOMJDD8mP9Osuk2DdDVjmxECkI/cbK61pkhE4FkURgV72yJEjdc8880yv+++/Xxs2bJg0YsSIExRFtet1Likp4VRVRfLe8QguBGbGjBlTc3Nzdzz88MMh1TdmzJhxKSkp1R9//HHEkpCw6H7x59U3HDxejbhlh9qYzKgf15w+Fk05U74gFCuyDGVVVOILSqpHVNSgohJR1TRYjZIoa6JV4Jin/9+18zPj4hqLi48m64r88PLli/c8/8Jv4f8D4CGhwo0GRDAQnIbD1Nx+1qF3u1AXdVdgNfUP+VIURfGSJHliY2O9CMsge8FisTiOHDkS88EHH2Tl5OQE8/LyduXk5EQM+7QcLKS5KIriQ6Jfy8/69+9/7dChQz3vv/9+SELdf//9/cvLyxM//fRTrPizVB2A9fCrxdeXHquEKmq3CRwjcAwl8Cwt1HmlajhRk1xCml2g4yVF9wJQsqoHdZ3oIPSQXALHag/fMPDlYLDBr6qqJeiLe17XyP4WufpwwoJOwNcHqQXLsU160O7LnscFXQksWDEQ27BsMKEd1vdwGdhsNjtFUTbkkiNEw7KsVVGUQEVFReyqVauQCZA2Y8aMD3Nzcw9gsuHhbm1cAEye5+2RSP+cOXMS09LSevz+978PZWtOnTo1XVXVvoWFhUhfidh+9edV+fvKa8dpHaBYLhsXbfqpwm8WY+fiHRYWHImIiuaXlVD6DaWommK38sHf3DLg/yRJgutAOnpUtV933ZD6D/+9acxNs8Yg4Q/5aOBZ8GFFCutAJeIaXNueBX0ecPrvV7sSWHgqOAF2/ELnwwSGNdcpU3jRokXMwIEDmZiYGPb06dOyoihWlmWpI0eODF6yZMkPkjOTq0lvsjc9Ln3tg9MebJlSHKpVtXHjRpaiqN5jx46NlA7DgrAPHjx486uvvlo7evToJJ7nx65fvx6+rIhgnftm8ZX7jtTcKIFqt9E4huZ4lrL4RPUsxy5A5LKxsXaBjoEKxG0kRQvCUZoUY6++N7/nPzRN89TW1spWq5X2N8YsrK6pqrztjmueN7aztfS0A2hw28AlgUgFpFeXeeO7Gljhw46wBFYSLEGQSnCYdjlSWxP3+eefx647se71erb+VFp02pbHvvfYwhbXg3vAQCjfuHFjxtixYw9HkmwZGRkFWVlZdcuWLSuZN28ee+211/bOzc0Nz9hsdtuVJYddf/3Pzl95A1Kb0gBedYqi9YCkRCTRAFe8k0tmaUqAGtQ0XYGXvn/P2L3Xj4hdKstyEPxSEAStsd52rSTqlRMnZ4VLUrhs0EeEvaAhIKHgEG4N8OCwcKKatcMuiLTCTS4msMxO4B0AMMQFETNcW7Sy7G5dU49NnNy/qDM9hUth3gfzbgjqwazs+Owdw2OH7+E4zj1w4EDT2w5vdGgr2dKlS2tdLteZSGGhN954g8tKTB84YeY0rHRqyQtv/ZjzeBZOmfdwROmKAPjPnl82u7yqEV7wVlu0nYtDwBmB5tYuYhmaibaxcRRFOIqiVJam9asHJSy8Ipk9wXGc1+l0NprpP2tWlV6javQNlK7PfPa5R55cWfQZXCIIicHwiCRd0X9IbezTRDIlFjPAhXyzC6oiuxJYUIEovQhPMOJ+rcWzmKIVpUtohtRYnQ0PLV++vD6Sz6m1iUHaCiL/oCfgUjabzalpmlWSpKDdbpcbGxvl2267rTdN0ylvvvnm1mnTpp1VDghA+fih3813JCV9lf/oj97/9PGX7hcstoVTfvuTVo2DeW8VD9pztO42vyip8FNRFIEACo0vCDjIuE1g7H5RCUC9tQVABKKdFgaLjPRIcJ68c0L6J4qiVIuiSMPlIssyjXx6d53tUV2jryNE/4TSqE9yp2ShDleorVtWluCTAxOm3jAEbhuAB++CRQVQgz+eZbh0ZhG3d21XAsuUkOgkdplg9ZjlrJF71WwVYxuUYK/5ymq1WjVNq8bGiPY609rn2NGMFBqXy8WoqhojCIL+wQcfZBw4cCCpR48eS1955ZWzBnn1/701Xo+11Ey6Z/Y+cwtXpAxUAzgYR/vjz398/5nKhmFEVmyUqgqUpkE6EJ2hZI1hg6zVors17oSfohvgn2qrP1CbidHW2LxBKYt6xCplwCrABK7kdrvrnU4n5al3jcjNzwzV+Fq1an8cq9HjdYoerxMynug63DVk7uP3Dti0aR24JhZyhw2mcx3rcDV0vvc4n++DzINrQQ1icqDrLZs2bToVCAT8mEhsapAkCVus2sxm6OxLwNJcvHjxWL3RO2o4l3gqJSb+yPQ//noz1A/uhVikJEkx2JCBbIqcnJxjkVJndF23fPzQ/Gu8VdXDNIZN2OPqNbhBVLB4zmocz1k0TZdUlvMELLZTjbRQobZiSvIczVwzKLlsXD+hBJszaJr2SJLkxX5HWMX4HY5e0ZfwB13XUWQEixXDeIhQZB2laeskoq+bPLk/NESXt66UWFBRWMHQ5a2tHDhGuS1btjgYhnHIsuzRNK0xJSVFr62tTfN4PKdyc3MvmPcYqTUfP/nKszZJi43lhMr0nCtfGv+LOSF1B0eqLMvYrHp827ZtAJa5jzE0SVC5xb97LfPkwSOTxbrGeEX+2iLUExJcZa70QR5JgVXWrLEsY1UUNZR2TTMspVqsdfUWx8Hg11kOTY3nWbpPaty2F36eu2LTpk3Jxq4fhmGYIMMw7sbGRrhbbCDyQV/sn3Sd9gBMRKbWTZyW2ew9w24bkp5GQVwYTCDt4JDfiKXYlcAyy/egUyCXmAj4XEzi2Ew1wBe1c+dOkPpoURQDWJ0Mw7hGjx59wVYguNS/f/zYvZ5ad5+oOKctdfCwp8Y/eGuIc+H5AFRVVdXJxMTEpJycnKYzc/C9T+c+P7r2YPlU0eM/my/FJ0QdjUnNbpB1h6aF0pJDLRxY5v9RFkH02FwHGjU6VMXZbuHY3ilxX/zhvglFiCQYWRzIEsU2Mn8wGIy2WCwNNTU1teGqeePGE1bJ7x9EdGrQR5/9q/Tll+fB0IAFDIBjnrGw8a5wdQB852WBtycCuxJY4e8CfmVag8gxAn/CPkIQ/C/27t0LEKLj0sCBAyUEnTmOgwQTGIap7Mg+v/Y6bn6+7uVFCbXlpQMdfXopiVcPPTh06FAz155s27YtQ5blKrvdbh08eHAoCA1J9dlv/nhV1YEjU+RAsFUSLthtbEVKz4zTtCNVFGVN1zXCcaxFls92NdA8rwRi4/fRglDaLyl+zf/+aNwBUyXjmTt27MDiSuB5HjxUFgRBDQQCIPf+gMeeLSvM60QPOZ9DbdfOLT/8xa9mm9mmrdUz7egQndN1FwtYbb4sgAQuoaqqlWGYAGoiIN0Yq09VVaTK7AeZR9bm0xtezZSDis3hsJ/59ZgfRayx0NGRKSkp6Wm1WuvgnjAlFsdxHlmWRRPMS+b9aVDVrrJZoi+CpGrxIIZhKM3lstVHJ6a4GWtMgGUTJEkJhWtwKSxHC01JTqI0JvHKke/9dMbvU7OzI6ombBBBPr9B4tUhQ4bU7Nu3zxYIBCyeOuc8otM7dKLvkUlgz+TJbSc/dnQ8zue6bxpYiF/NNDzDEMWQBlBlAAkkFAa4yX9SWHggtaCgf7MSPUbQOJTHDmBhfwJWqtVqrfrTsQU3Nni9fYOaqDp4G51qS13yf1N/ibSRc2orVqywx8XFxUHtwZKMjo5OlySJMpMJsa3s3Tse+Zm/tgG55Z1qrMCylti4WK+qBVWKYSlN01lFFplgQAolx6iaFtMz/eAtbzyxGHlXkW6O3dYoQOJwwN4hvCzLdaa1XFxcGp+bexYoMVbYGoYvYPyRnYvxR4Zum1ZppzoX4eJvGlgtHwkCCTWHDsMShHcY/OHLhQvX6klxKeAx26JiG2eg0AbLsqqqqjpqKwQCAahC+6uvvjpSluXRQ0cOsx6zVvSTnUxNDeM5oOiq0sOZUvHG9U//NUISX4fHCUFvv9/vSUpKkmpra3tiBzN2UYdU4EPPTqs4eHQk3qnDNzQuhE+Lc9qipUZfpBMxQlcJNiuTNLjfoulPP9zqzmbj/ViWZRuw2FRVZYLeuHcqKk7uv31O3j+NSAb4lVk7FXOMBY0wGp7dJaqxq4HV6nwUFx68UidaT4pQmSk99TcDgQCsIMrr9YbeUdM0h9VqtYui6LRarSm7zuxzbajaeZPfE7AF4/TdHMOyCba46vsybnntiiuu6ExB/mbvhM2mdXV1UQkJCTWVlZUZPM/XIlhdUVFh//yBZx8JuD1Y+Z1uNEOQtYqRAAAgAElEQVTTnNPuEhs8rQILN41OTzox6+35oWzRSA+BBFcUJcnlcgXQT/zdWOu8n+hUed6UrA87/WLf0Be6AlgdPgMQ4CIa7c2dknEIweb09HRINCvP8w5BEKIhvnw+X7UkSXUTJkxg7vr4kf+p9DWEzHq7YGEzXD333BI3aS1UJsdxtZE2WsDvtGfhpy6fz0dG33s7HKPBlvFCFEuzWCzeYDDYS9f1E8ix/88v/zCuat+hyaZbobPzQTM0y9gsNtnjb9PjDdKfMX70q6bbI9JzMDZ9+/ZNlCQJIK+TvUnpEiVZWJ0Scgv6hxcHCU/3xlyb7p7Ovn6nr+8KYGEHCWJTCOJC7cG6gq6HJxixNahGmMArVheWFtO0vssZ7f09wzCwfOBigO+GAmn1+/3B8Nje06tf7lcp1udQumJlGb7ihcmPrcZKh1NV07QEZPmG17Za8sizI7z17rxAgy8ajIN32IOcQ9hwyyvz1oQ7P82NGogJK4pyeOzYse7FP3vijtojJ5GNeU6N5lmB4VhW9gXb3FWEvqYN6bd6+nO/aTVNx3wB1KrQNC3K73H9QlOpX9TWVr1+y+1Xf2aoQYwvFh0C0nChoHQBLMmzTjM7pw6186WuAFaH33vVqtKRtEaicvOz4MNBgI3at28fds9EUxQVqnfV8mZGbBCBuWYRfIBD0zQkvcmjRo2qLH7xHdfp7QceaaysbkZanQkuwZGc8N7MP85tdooWinsoioJ0Y9upU6fY6tXbbhT3lXeo6kykDgvRzhglEAyootyugze+b88DN7/2xKKObJLFs4oKy66lKIKdHGJ+fib2DFz01p2Axa5etmcqzXM2zlK9zOl0WimKcui67q2rq6trLU7X1ggaTlYYCaR63VcDjq/Zco3i84uECgWpKYphENSlU0b3P5I2/dr/oGAay7KQkLQoijxcGzRNT3a73QOOfbI2i65u3KaJsl9T1VBYGdJFV1Tl6yCzjv3ysHMjpqhwTluUGpQCmqy0m0UQlZJ4+o6/P/u38zFCLjayugpY2B0MkQziioFH3VCIajw/lBUJNfn+v9Zfn5CQSDlc7iewQWLEiBG+cxxccAn8hOo+ZGRk9JoxctxMa11wdK3f60yLTvClCc4TuhpCgpY0OPNY39sKFlIUJfj9frckSfrJkyfV3r17xyqKIlm9ctyONz/4oa4TTpUk7FimQMYJTTMEnvWvYQq4MhShvkaYpqka8ow5yqlrROEJJUreQId2KEfFx9bdseD51zuSw3+xAdTa87sKWHi+WfW3VY6BjQKi6JemTGletvEcBg9cAoctIVxkmTVr1qlpA0ZdEyw9Nkar9bl1TW9Sh7TA03GZaZtu+uNjy1uS+B07dvQuKys70d+WElXy9sJHRF/rnnbzHSElTdDh3xpG7nu4riJeUOkqd6NbkyVZ7RUVX5tki/KB59k5y1kS7DKwzmHGu/or5maM6Ojohk1PvXmvp7bGpQbVJmA5k+KE3iMyXrv6oZ80xQLxjihcO2PGjL5G2W7rOzc/8NuIccEOdIjmWI532lyQdAG3x+cPeOWjDXUxbiVo65OQ5InvOYCVBasFepQLBgJpLm7vTX96DP64NuN5qDevKApXV239X6JRh3ILMlG6u1u0rpRYXd7hEydOWCsqKlJ4nq+E62HpvD8ki7WBiUGPL5UihOYFvkZwOTde94dfn0XKYRRs377dBJbwzzsfecBb0xByeZ9L46PsMaqsSKzA86ooiQxFi1VJvXqfZm1poqIyqqrpSAukaZayxblOW3umv/XMT3LXRwIXPPCw+MAPUfO0sS7q35u2rP147mM/QrYCNAIiA3BrwMuO35FY2aX1G761wDJifT0w8OG7cQwrEv4xeM/VlhwOmQs1pTXWHYs/TGbTYvqqVQ37J/36xzWL7nvilrrDJxEkP6fG2iwOXVElcC9LXHTM0eiU9FMiE2NUW266J0XRRIpyHXVz9hO9U6N2v/hAwacmuBYtWsT37NkzBlmkLperITMzs8knhhBUbi6OsA5FNczjUeBDNCsAAozwa2EHdXgpg3PqT3tf6lbAKl5R+gOd0Hk8559viZJrJUlCXVjZYrEE2yr8satil331qd0pgsqK942cdebJJ5/Urr/++mSAqqM7pAG4Vc+9mV5fVn6tp76hvyarKme3upSg5OMEvj4qLVl2l59KDDR6zyndhLNZrCFrUtOl+n79Bx1X+FRZOtv1wLAsXRuVsMWv6V5IpP7pMeuf+/nE1fv27WMDgUAy/HmSJCGDFMVzWVUVWHcN85xKtJ2TCr4uQdAd2sUEFlaPGSvEqjpcuPTAAI6lX6Y57fdRMYF1OAgJITZBEKwej0d0Op3ult70eeteHnC45vjNoq5wNE0xKbbE0ntSZ3zh9/sb4DHvyCADVEsff3lY9d5DNwa9viYyzdmtTlWSg3AR8HaLINjsV4gB/17JG2jXZdDyubzDCteJrggWsju232hkKsCSVDVdIvp/PRS6zdZYZYneaWaWRtss6pNzxrxeVXUkymKx8DicIBgMhuJ9uq7Loi86R1WZp3bs3LTgkV/NgbGCz+AQxdwioH9Rzo3uKmCZEXboe7gc4HGHOwAiGx5h6P+zMkvhKtq3b1+oOh4qyyAYjVUqCEIAhWzx+c+XzLvzSMOJvizNMDzFWWMc0dYJKaNfnjPyBvOQyXaxtfoPb/Q7tmn3PS0BEw6sUBDZKmSyFotF9gf2ykGxU9kBrFWwwQ3RmNozqVRz9EF+FsUwLEMRRlWx41nTkFXqjYrZ16AzTQVIou2C85or4rcO683vtlqtjciqHTFiRGMbG3IRycCCxdyi3hi22gNgABsczOBbcNJ2qDJOu4PXygVdBSyEdQAcFFNry/OMdFmyfft2J7bVI3Ivy7KKzQ/4HTU6wYEoioqWJMnN8zy3eP/yh48dPz4oOjlWO2NpKBJsFvnqHsP+/mDOXa2l6DYbCuR0Lbzn0e+7T1Uh3NSs8U67U/EHApqqhSYB1h3HcyNZnjvqq2/s0HZ+84ac3WLXNF2tTMvsc1yisJE01EJuWoZmNUI0PtalHFcsayGtsA3fJrBWK0+5BvaL2zE+w17E83yDJEnYCY5x0DE2QW/sSxB4Ok2t5ihq9fhJmc0iCGEdwkJGJAJzgSrQndoo3FmAdRWw2novbCuHBAPpBH+pLikpqRoxYgSCwyEdgQg+x3FYhTGiKIb2dW7YsGHg/v37xzqz4pNqU6XAGaU2BKQER5wyf+aDf+xB9ehQesj2Vxambl+1/r5I2aB8lN2l+AIeODqbAGIREgWHPT3oadypiG3vfA7vNDzvlKYrp1L69CmXGMRKmzXObteFRL53XU2VzNnij1lccQ3YCS3KanBA77ht04fHLxNFsXbJkiVBczscCLuups8lmj6eEDLRuOFRneiraZ2sZqz06vHjMy/KafcXA1iQDOYBkEjeQ9YnxHNTPQdYdEUr98/krbVrrFarBQl2WKAIt7z33nu99u7dO3DkyJHe/Px8OiEhYfkb5R+NDypSKsuwgURr7LZ5uQ9gB3CH2qe/eWlkxa6910XKsUJ8r2WaC1DtSIxN1xStyldb32ETHmpVl+RATXq/3odVvpl0pDhB9Thde5D33iuGGR5wV6ZVnj4ux/YYcIy1ujyD+iUsyc227TEiR0hNxnk9otVqDSB1Gx1dtGijNT4mPo8QfSLRqImECm2tJ5Iobp0yY/ANRvC/Q/W7OjRw7Vx0MYAFvgVCiUlp2VEQ+riVy/d9yHLM6diE4IM+n89jHrCE3G+cpgWQ6bqebrVaDwwZMiSU3wQViX/Cc8U7MkCf/PIP11TsLp1k1GJv+go4ER9lj/ZX1p116KQtNkpPGdz/i5Mle3I7kqKMm4aC0P6gT3bF2vdEpQ6TjV09lGCRGm3OAx6daVJNqTFCH0qV7adPHVUDDbW8RT62+Jn/nbsMVZ+NfCwr8vA1TbMNHToUNbHMTRJN779y5Z6erM7n6YRckVeQ9YKxWRjzjUXcarmAjoxZR665GMCK9F5msRCEfRxLPtmRI9gtK/LzrwhlUiL5zu12x+u6HspuUBRFsFgsXMstWR3pcMtrPp/74vDju/bP1IyJNj+vIME+uqaqKbS9mUcenztio72zF/7x1VW/+0vvyn1HJ/saG2Nbfv8sVYcgtD/oZzhGL++RPbBC4eKw/atBcJQFtK/7ZTYcJOCwMMjo0NMSndtnjohdxLIsdnSLFoulMfwIPCM1BuUhQdoBGgC0NfUXKhRsHNgO6oAYLrgiirN0KI7Z0TG+mMBCJ1FaB7lakGDwEjdZQ0UrD06nKb2X1dmAGF4Ap06cOnVKSUhIQLVkERssOupOaGswSv71WfzuxSseCpc8rMALezwVmSmc46SL4s+qDZ/QJ730ptefRFoL0hwsHz40/1p/Rc0wyee3IxYY6XlQhURRAzRD6bYe6Y2b4volHwlQ/kg7okHc45xCQmKMreKHBX0X1tfXh7JYkWfm8Xhcdrudb6yxjVcJ5c3Lz/rIeB7GE5EBqEC8AzimCbTWhgBSHmoZdbVQJ6NTlm5b49qVwIKaQ8exSmAVYYWAV8H3Ep5DjuS0Kz//bPf7gsVS6YxpnIg8LORX6bqerKpqDcuyoePZLsTmVajQxfc9fmvt4VNZDM/xNMcKHjkg1Hob2d4xiZ6WiXnIS08b1X/B5Ln/5XHghJAYH/3q+QFUINDPX+9LUFXRqasapAhhGM7vSEukWbvlOE2zO6Y98fNjH68+4CzcfmRGldvfLygqzXPE7Lx1QJqrYerIpLWsLocOiMIBmzRNIydNRoyw8hS7/Mzp8uI778rHGUCQeOG+NYw1tAD4V6d9bh2VSt0FWFgZCCvA5YDk/pYbEhB+wMpB2GTPqs8P9Jo0pX/x2hWHenDOKh82q/r9/mqO4yiWZV2tHacbqbPwd31t2f+3UrKRJYrtZbxUX59c/sH62701dTzyrcrrzvB1AZ9j1MArKbHWXf1fdwNNx/frvePGP/12SWs56UbICM/D5JoLV0fCYl1dnXjNNdc05byHtq/9tTizTtEyRb+MjREk2mmrT4gVjkwe4EQKTyMyaaurq08lJiZifOJ5nq+rOcUn5k3tX/qXvyyIue++O2EI4VxD1HiHCmzaF3khAHKu9+hKidXaO8KNAN8KLERUQWnS9atXlD5LUfpYR3TjLJqmaz0ej26z2XoYm1Y7VCTk6RUr+hyrqR+tqLrdwrA1N13Rb2usprHm6ad2u1202WzK6U++TD2+fcdt/rpG6+6K44k2Cy9lJqT7WQvYtc/NWQQmumfyzpteeRyg6rA1aHYaW8tcLldMpAVhVsgxrtXWrFnDR0VFhSxHXderkX48cuTIk8uXL+fj4+NjvG7XW4qsHC2YNvDBsAUK4OGUezidQS2QgnzR2sUCFlY0gARAIexiFroPLy+tP/LI79IK8r53N2Hjnne71wV79+6dKoqiN3zVtzVyyG745fLVj5z2eEJ1C1wWIapvtKvy/lHDXwsP4Jr3gFvjwwefmbRgzdKZo9MyG+IFR4CPsjltcdHHbRZr8dRnH97TmqTqyAzu2rWrz+p9SvovZg3/sq0ERgCtpKSkN/L9BUFo9HpRC0SwDB06FERbX7Pq0K/fX/TOjtf/Oh+8FO4a8KnwY2JANTC24Fi4Biqx01vWOtKn1q7pamBBPSCTFKQdA4KBaskNQOZR3wGWSigss3rlwQdi4ryfBoNBuB467DGe/9ln/b84VX2nGAzSVpa1KJqmWjlOfuOmGc8mJiZGtILi4+NTWZbNXPLeezut9Soz4JbJgePHj0dXVlZasrKy6hcdPhx3sqIWnn/lyt5p1bOGDWugKKpD0vPlD9YOO3YmeHeU98gL8x79GTaNRmwAFs6NdjgcVW63m4eRsnfv3lhsfWusddw6IT8L5SHR4GiFgxnOZRRRa/kesLJRhQYLtumMoPMBTEe/29XAAqEEsMAHwlcQBgZxLUgx+FjMY3ZD58F8vvSrQl7gP8mblD2/ox3Ddc8tL8peX7r/LmfAf5UtLt5T5vGWxEU5uNfuvWt+MkW1uVsm/Dk40uT3ny6bWO5pHHe8wc0ohFZ1VdV5hmbinLajo/pnrfv5qFGHOrL54ScPPpZZtmfjoJ49exb//e9/j3gaGZ6N7f4ul6vS4/Ekm7Xti1aW/oLo1Au6TtZTFP1oXkEGjsHDHCJjFjUwYFVj/MK3mGExwyDqtPruzFi3vLargRXpXVHGGtYT/Crh/heACgHUwD//sSJz9g8mL+lMR7H3Ljs7O+7fe0pfKy8/mlzOCKscTjuTarOXvfX92xd0NJceoLr/ww/zj1TWX6WrKo96Cz5JbgZKp5XncjL6fDwvP397R8A1ffr0vpqmZfTv33/9iy++GDH0tHPnzixJkhrhZkF9MK83hs7NzTi06vMDuQzNzN9/cNfy++6/+Y1wF42xMEHk0c46irgz43e+114sYOG5qI6CTRXYrmQeoG32B6oSBflxsmmrkgXW3rZt27CZ1eLz+ULpNSh5xLIs3BrYtjXi488+m+gYObIoaI9xCwxX8+dZM7/oDPn+1aefjtl78swMj1G41iXwLr+i+mVVbWbGJzvt1hn9M16aM358h4LTd911V+/6+vqMYcOGrYl0ABScwl6v14Ha9Sh5KQUTPiEqORkV5/xZTk4qVB4WI2gDJD8yYE0NcFEkVHeRWAAW+AEkVLhKxP8hII0QBdJsI/pgDEDFIMsBaSTR0dH+2NhY/fjx4wgXuRiG0U6ePMkvWLBg9I033niyV69eRaNHj/Z2RJq0UIHW2X9f8JMTdfWh+utoPEMLAstyHlFqxtFYliX9EhK+evP2m/7TUWn46KOP9l+3bl3fDRs2rIzUV6jDYDBYj026awrL5hw9cbjH3T+cgtPJkMGAcBjGEfQBkh0Hhl6U3KtI0u1iSayW74LVN8jgAeagtSqNN2/e3IdhGM+RI0fqb731VhXEFvWiaJpuxAEDK1asiFqxYsWVo0ePdt94441nKIra04Gj58563rslJT0Xb93xE7c/2AzgMRZLTIMoNrSML/aIifH/8+47sW2ro4VjqZtvvjm/pqbGv2bNGpx80azhrGtUMgwLXZlHGIOTwtozyTrGz6zpDpB2KZ/qzsACoUc7K+Db4qVRQjpx48aN+xCYRqnH2traBFRDHjRoUM3mzZvtbKgGlXTaarUmYYu9LMsJiYmJpX369Gl3B3LLAXpq6dLBXx45eZtPkpolxTkF3hGUZUlG9mdYi7PZuI9+es+zFEV1Ku5WUlKCrfvuSGnUAFefPn0giSHZTcoAVY/vwAfY8uheSC+4cGAldlk2Q3dRhefCDeEwBDjAuQLFxcUOh8ORSFFULYqioY4BPNMej+d4SkoKDhhHKnCULMsUz/Pl51J1+enlRdkbyg7O9svN438DeeZORdMCpYpuxulC/Ylz2LiPfnzP7xDb7EwHERLavHlzms1m85nZGi2+D0kFPgorEpYfAAPfHHZ5I6iMxD1TSpl1sBDBwJmFFyz+15k+dRdV2NY7w1SGKwKrEwPYpJY2btxoheTCEXMMw8QfPXr0OFQjSjzqun4aJ7AKgiDhcPhWJqzNsVp5+LDrpc+LfukJNt+o2k+RbiWqYiu3OReEk/jkaFfF+/fMwdb4Tm+4QNIez/NpgiA0tFIKE4ABWKD2zCxRzB/4H+rnA0ThKhDAg3vnovCu7g4svB/UHwYJnALqwIzDARRyUeHBp1hOPaKSin+ivgNO9lJVVXI4HB5RFFOwowXJguG1RTu68pC5cM+7C28+XFML6ysUbIy1CHEJujraXXEmytG73z6votS4Ramepih1SI+01c/eMB0Vb87Jy71s2TIhyt57pigyIycWZP9PK+8JnxWsZjiPTfVuZjXgbxg9nQZ2R8eko9d1Z2ABTEgBwUo1az4hiI2TvuCjgVoQ/vWPoh8mJaclTJyc/SQkl6ZpTtRmRx1TFO0IBoMiSlePGTOm1RNS2xqsv23Z0uOznXvuliQ5ys6yUdECn6zJMu+pq2Wcickenei6Qihvmt1WfUtW3yW6rtdrmsawLIs6pqETU1mWZXByFwCPJMW4uDjRPLak5bOLVpU+Wnmmkrp9zvg/t3F6BALPkF7w3pvn4GAu4cMyN0x0FAPfyHXdFVgg8/BzhR/NgVWJ7AeoQ5OUonA+iPJXxYWlj+iUlm2x1/8/qEcU/UdWQHp6Og4CYDq6v9AcZahZl8sFruaqYpixaw4enVbr91OiqoqyGGRO7/0qNvmKQZVOl5NJdToqbs3K2ExUFYcM8Niq5nK5xEAggNNfIegCfr8/EB0draiqioRFCSfDCoJQF6k4nBGdgJW8vo3SjqYljUTEi5LX3hYiuyOwsBIBKpysCs5g8oiRhjMVg2hKMwzul8WfH5ii0/QyQsjzeQVZvy5euefq2EQ1VFp77969yfX19b5IhzGFDwzUEI5XQfkkOFc1TUP+k4DAtMVi8UiaFr/hTM2Q8gZ3j8qGeltd+TFHxqDBZVnRrsNTsjNKPR4PJJIGYwGZrhzHYVcR6tNLZj49z/POhoaGhtzc3AYk7fn9/gSO4+pb4VSmykOWQmtbtTAOWGQXzfprDVzdEVgYUHAE0+MO8g6LECvTtHCgDqEim4qMvf/PonG3zc7bULSy9PtEp/5BU+SeCflZ78CUh6XYWn0tWJdOp9NpAAg1T7G9SrVYLJQoijgLMcRXkBeFWl1OpxOg03w+H4PUm0AgAFUX9Pv9BNKJ53mc1wNVWAdAWa1WRhRFC84DcrlcdHV1NSSWPG7cOICe9/v96SNHjkTstGUzj4jDljj0/aIk7J2rnuyOwArvCyTSOELI7rCjOZD5AF8NUmmxksE3QK63YOUWFZZO0wm5fWJB9hxwLgBh4MCByJRo1iAxZFmOw1G4yO+y2+2s3+9HFb96t9stwGURCAR8NE3bsfPYZrMB4JBEKMpGW63WWhgHgiDgX/A5cB17IBCgAoGAm+O4XqhsDG6HTSCw3lRVPQVH7caNG9NEUfRBchlqD2oe4IokmWARo2Hn0TkZBecKjvP5XncGFqxBqETwDNOMRlozeBai+ljBpjUE8xuTFNqp88ADL7OvvPIgpBv+PssxijicKIoAZBXLsjJqIlitVskNRAlCGsuyjQAPQJWamnqmsrIyMT4+vrKuri7O5/PVWiyWGLfbXeV0OqN5nlcZhpHdbrcLRgNAw/O8F+oNVWEgnZD2sn79+hhYp8a51ZBGCF0hdQhggpGCjI5IFZXNuCpSYMAvL4pfqrMg687AgsPTrPaHfoF7AVSwEJGTZVpBOJfHDKGMMj5D6ggkG7zTzUIl61YevkmI8nzl99eXI2ce8TjD6w0g9MBJFCjODJPecFVoqO6Cs2ucTmcvhFcMiVPpdDp5ZHdio8OGDRt6URRV1dDQoGHDB04LW7x4MdWnT59eXnf0VbmTMlGD3QwQQ70iEQ+GBwCF7E+cJQhveSSpBR8e1D9cLt/IoUqdBU5713dnYIW/O4rfQ3oBVJBUmCB4ovG7mdsFUxsThGAsGhLcMBHNEgNXryj9mKZIem5B9kioKIAG5+SgmK3f7+ehujZs2ACPvoKkwk2bNqWDL+GG2NOI1GIUczPOUJQBqHHjxh3H9xsaGnCedPWmTZuSAt7oa3In9f+gqPBgMUWInFuQVWAsDtSvgOQBd8IO5hUGmBCAhxRtrYAupC9CO6Es0vYm9mJ/fikAC+8IaYX4l3lCOwKuUIuIk6EhKIsVb57oAHcF1CQkQFNbvXRfL4pjj+kUdd/E/MzX8AHSlw8ckHielh/TdLJa9ck7XKlBu9frLZ8wYYJeUlLSC+QafA2ebAAPTliXy1UHXxSMA7/f1WizuXFSRCpOsUDGK6WTlymOizl6aP/we340DRscQrttjAWB36GiYZSgf2aMFLlp8Le1TCMy+4BrsXg6FTK6GCC7FIDVclygIq/G2dGGKoEnHiENrGS4IsBFoBJx8mgzfvXmqx9fqRLyw/4Dxj2am5sIroKJ3Fm86tB4XdOWMxQZoKpkGKHInzmb0E8OiL8gRM/IK8i+w+BIIX9Y0coDCyiKrl77xb8eHj/ujipKJ7/NLchC0l3osIS1Kw70UCn6CEXTs3InZbxPCIGrBCDHwoDkxTuDF8I4AdeCOodaNP+GFdjtwdMWYC81YAFU4BqwAE3QwCJEP0yJAF4F1RWJCINPAXiwsAACqJ8TyHVSiX7VxIKsnxUVlj5JCHVvXkFWWnHhwf+nEz0xryD7t+GDWFxY9qVOtL15Bdn3Fq04CD73Ud7krF8ZoIHEaZgy6ZarP1+1GECCFIWzEzwQgIGFCOln5vtDvUFyQYXDHwVJDGmL+14SRD0SwC41YGHQEbIwQQPuBWmAQ7YxCfCBQQrBFRGpQZLB4QhyDksMUgGAhBqFOv2qaGXZv3VNS5w4OTvPAAQmHvdDFWYAuvHWW++ZlBiVevjPb/3uaFHhQXAkb15B1k2G5MQ9wfuQdYD3w/3NqAHAA34EdwkkFDgg+CLeBS4R/ECahSzWS4FLtSa1LjVghfcDltJUw0NvWoVQifg9EkfB5ILgm3FHgAx59uBuACPA4P7g/S9vtQh85nUzRzxjTDCkCCQgeB3+hcEAqYisgaqPF2352Y49m+ueeuoBqDzEMiGNoPbgwYcVCzIOSw8gQ8PzcA38UwAqgIZrAS682yUrpcIn51IGFhynAJBZtAOTigkHt4o0OQAP/GHgNpAmmHR47mFtTSGEIPMS0gYcCJIEUi10qoXhEoBkREYBgAuJAkmGewGwkHhw4oIjQaqannR8H8+EJILahSULHxykFJ4PkF0S7oPOGgCXMrBa9hV9wU+kuBmkG9wPMPOhSsMzVgEMGAM4FAmfYRMHAASQATBoAAqkHSQcJBYIN4AFiYPvmwFzgBSOXagxABO/A2gAO1QcuBbuBWkHT3TJCVoAAAHwSURBVL5ZcqCz89btr/82AautwQaQ4Dcy65KCLwFksCIBHkgwJMqB0M8wOBt4XDiwQPxBzCGBcD0+M78z3AAPQA1jAioTPzA2cNATLFgYG9j7B4foWSGmbo+UTr7gdwVYIOYABLgOpNcEY7LxfwAdLDWoNUgRqChwJKhTgAeuAIAChNusPIjrIdnWGOMN/oWQEu4HCQW1Zzpqof4AYAAVUgvcCqGcVjerdnIOu+Xl3xVghQ8+1BjABfCg/+Be4FSYeKgmkGyADCAASCBdEILBZ7gG4AEAYSjgOnwGqQSuB0cn7o3PzMwLqEoQdKhZ/Aug4R7mbu9uCYzzfanvGrBAmjHpkBgACTgRpI95hjLcFYgxRqo8jO8hYxPcCeQdgAThRzOLx0FVmnwOUQEACMAyU4khBQFKAOwbLYd9vsA43+9/14DV3niBkAN8kTgQHKtQiaZxgJJBcGJCVUKd4if82FzzWW0ZFe29zyX7+WVgNZ86ePVhsUVKvGs5yfCDQZ1BSkF9QsWasctLFhAX6sUvA6v5SIa7GtobY6g3+KGgGuHgBCjhVrjcwkoZXh6Mr8EBhyak1blsnwIo4bDt0Pk93/YBvyyxLtwMw01hVte7cHe9RO90GViX6MR199e+DKzuPkOX6PtdBtYlOnHd/bX/PwGHGxc0kZ8pAAAAAElFTkSuQmCC"
},
"dataset": [
{
"key": "__0__",
"name": "label",
"description": "",
"type": "text",
"kind": "column"
},
{
"key": "__1__",
"name": "id",
"description": "",
"type": "numeric",
"kind": "column"
},
{
"key": "__2__",
"name": "children",
"description": "",
"type": "numeric",
"kind": "measure"
},
{
"key": "__3__",
"name": "Size",
"description": "",
"type": "numeric",
"kind": "measure"
},
{
"key": "__4__",
"name": "parentid",
"description": "",
"type": "numeric",
"kind": "measure"
},
{
"key": "__5__",
"name": "Width",
"description": "",
"type": "numeric",
"kind": "measure"
},
{
"key": "__6__",
"name": "Sum",
"description": "",
"type": "numeric",
"kind": "measure"
}
]
},
"config": {
"autosize": {
"type": "fit",
"contains": "padding"
}
},
"data": [
{
"name": "dataset",
"transform": [
{
"type": "stratify",
"key": "__1__",
"parentKey": "__4__"
},
{
"type": "tree",
"method": {
"signal": "layout"
},
"size": [
1,
{"signal": "radius"}
],
"as": [
"alpha",
"radius",
"depth",
"__2__"
]
},
{
"type": "formula",
"expr": "(rotate + extent * datum.alpha + 270) % 360",
"as": "angle"
},
{
"type": "formula",
"expr": "PI * datum.angle / 180",
"as": "radians"
},
{
"type": "formula",
"expr": "inrange(datum.angle, [90, 270])",
"as": "leftside"
},
{
"type": "formula",
"expr": "originX + datum.radius * cos(datum.radians)",
"as": "x"
},
{
"type": "formula",
"expr": "originY + datum.radius * sin(datum.radians)",
"as": "y"
},
{
"type": "formula",
"expr": "datum.x + 100",
"as": "barsxoffset"
},
{
"type": "formula",
"expr": "datum.y + 100",
"as": "barsyoffset"
}
]
},
{
"name": "links",
"source": "dataset",
"transform": [
{"type": "treelinks"},
{
"type": "linkpath",
"shape": {"signal": "links"},
"orient": "radial",
"sourceX": "source.radians",
"sourceY": "source.radius",
"targetX": "target.radians",
"targetY": "target.radius"
}
]
},
{
"name": "circles",
"source": "dataset",
"transform": [
{
"type": "filter",
"expr": "datum['__2__'] > 0"
}
]
},
{
"name": "bars",
"source": "dataset",
"transform": [
{
"type": "filter",
"expr": "datum['__2__'] == 0"
}
]
}
],
"signals": [
{"name": "labels", "value": true},
{"name": "radius", "value": 280},
{"name": "extent", "value": 360},
{"name": "rotate", "value": 0},
{
"name": "layout",
"value": "cluster"
},
{
"name": "links",
"value": "diagonal"
},
{
"name": "originX",
"update": "width / 2"
},
{
"name": "originY",
"update": "height / 2"
}
],
"scales": [
{
"name": "color",
"type": "linear",
"range": {"scheme": "set1"},
"domain": {
"data": "dataset",
"field": "__4__"
},
"zero": true
}
],
"marks": [
{
"type": "path",
"from": {"data": "links"},
"encode": {
"update": {
"x": {"signal": "originX"},
"y": {"signal": "originY"},
"path": {"field": "path"},
"stroke": {"value": "#ccc"}
}
}
},
{
"encode": {
"update": {
"x": {"field": "x"},
"fill": {
"field": "__4__",
"scale": "color"
},
"y": {"field": "y"}
},
"enter": {
"stroke": {"value": "#fff"},
"size": {
"field": "__3__",
"mult": 400
},
"opacity": {"value": 0.5}
}
},
"from": {"data": "circles"},
"type": "symbol"
},
{
"type": "arc",
"from": {"data": "bars"},
"encode": {
"enter": {
"fill": {"value": "#ffff33"},
"stroke": {
"value": "#bebada"
},
"opacity": {"value": 0.5}
},
"update": {
"x": {"field": "x"},
"y": {"field": "y"},
"startAngle": {
"signal": "datum.radians + 1.58"
},
"endAngle": {
"signal": "datum.radians + 1.58"
},
"innerRadius": {"value": 0},
"outerRadius": {
"field": "__5__"
},
"cornerRadius": {"value": 6},
"strokeWidth": {"value": 10},
"opacity": {"value": 1},
"hover": {
"opacity": {"value": 0.5}
}
}
}
},
{
"type": "text",
"from": {"data": "dataset"},
"encode": {
"enter": {
"text": {
"signal": "datum['__0__']+' '+format(datum['__6__'], '.1s')"
},
"fontSize": {"value": 9},
"baseline": {
"value": "middle"
},
"limit": {"value": 80}
},
"update": {
"x": {"field": "x"},
"y": {"field": "y"},
"dx": {
"signal": "(datum.leftside ? -5 - datum['__5__'] : 5 + datum['__5__']) "
},
"angle": {
"signal": "datum.leftside ? datum.angle - 180 : datum.angle"
},
"align": {
"signal": "datum.leftside ? 'right' : 'left'"
},
"opacity": {
"signal": "labels ? 1 : 0"
}
}
}
}
]
}
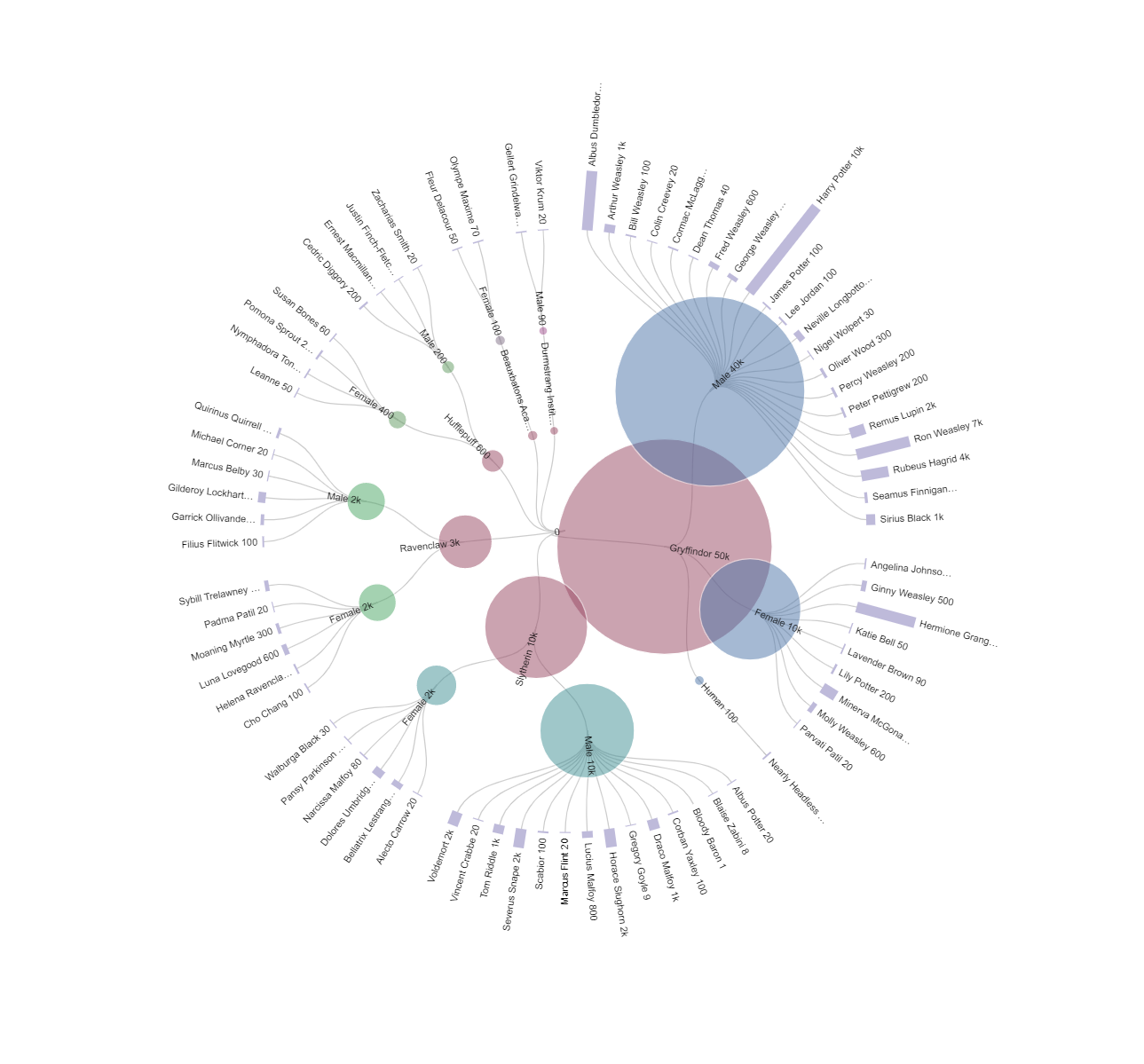

KK, how about wizards by wand… core, wood, length (rounded), rigidity?
Now if you can come up with Albus’ chosen wand composition, huge sapiophile points
“huge sapiophile points”? 😀 😀 😀
I have no idea who you are but I like you 🙂