{
"$schema": "https://vega.github.io/schema/vega-lite/v5.json",
"usermeta": {
"deneb": {
"build": "1.5.1.0",
"metaVersion": 1,
"provider": "vegaLite",
"providerVersion": "5.6.1"
},
"interactivity": {
"tooltip": true,
"contextMenu": true,
"selection": false,
"highlight": false,
"dataPointLimit": 50
},
"information": {
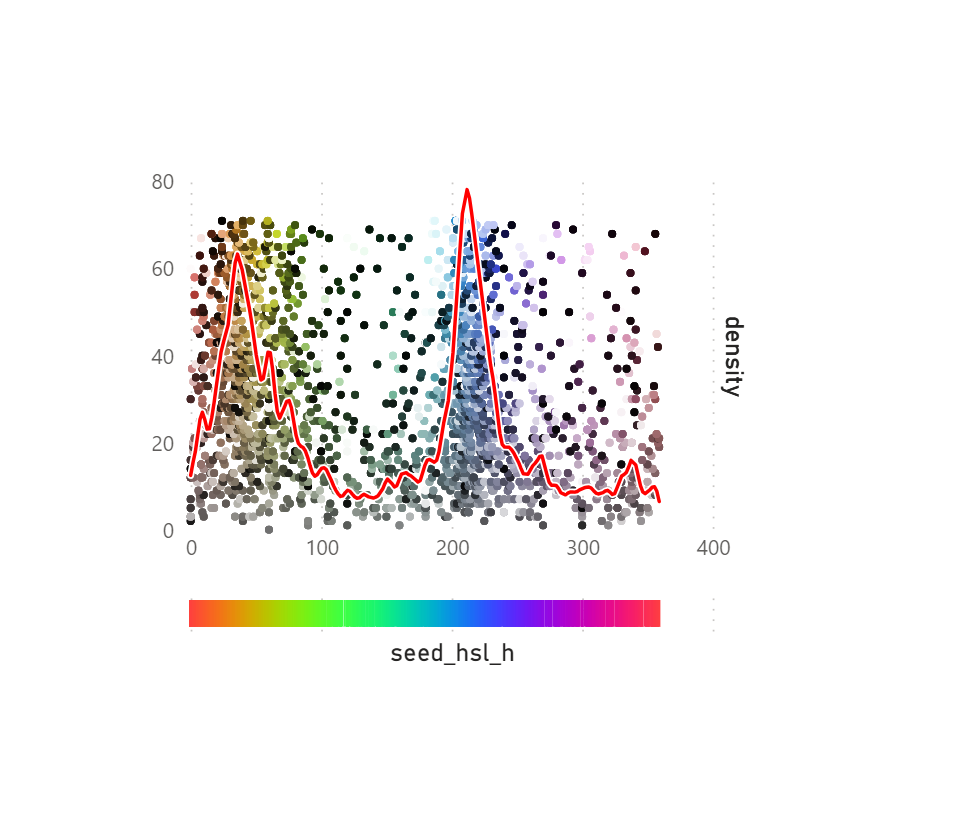
"name": "Strip Plot with Density",
"description": "[No Description Provided]",
"author": "Kerry Kolosko",
"uuid": "b9e7e229-25b3-4267-adef-f92002f0bda3",
"generated": "2023-07-21T16:26:24.157Z",
"previewImageBase64PNG": "data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAFgAAABJCAYAAAC5H+EKAAAAAXNSR0IArs4c6QAAIABJREFUeF7tfAd0E9fW7j4zGvVqufdesY2xMb33UAOYGggkQOghkEJuEuKEEBJC76GF3juYDqYYMM0GbOPeu2xZvWvmvCX/z3mEC4TkJv+7/3v3rKW1JM2ZXT7t+bTPPnsGwX/G34oAapE+bdo0vkqlsshkMmLLli22v1Xr/0fCmwGeNGmSFDFMNwbRJgBsFovl99atW2f5/wiHv83VZoCnTUuSmM1UG4QoPsEweqFUmu4AODU1VdqjRw/1v6o9JyeHbSopYSUMHmz8V2U9bxM+fDgAjRpV+mdl/lX+paamslwBuFE9euhftOVXiniZkX+VAX8HwHjaNCNERl5A8+YN/x8L8J81/L/jPDx2LA1RUQXoyy8j/jv0/Vkd/yMjuHtVVVsoKDgAYrEeffKJ/591/q+6Qv9KiogDgEyHQwPbQHxoOFe1ar+5xPH5wmnfqP5DKnJe5uxfQRFVSqO3t5xf5QCl7ZPsO4LKMhkWS2ji60Xe/2MBftFwikR2HkUW7/umP73hyPWIsDA2Awg9iOvJDXCSka5D3q5oviI6j5YkIQaNv3VEPezPOv/8eVUmi50BRPjy2MSBDIU9pDCLlFj1dEBVLnmt+7sFbFJQgGjSr1sHQQyA63A2id610vVDX9Qdymtzo8CU0e2vsOlNZbwxRSwb2G77lbomd3VTbeLOxcPkyVvOIGdn1r2Nx5XtRw2XqkPDKYnOhi6bgnnv1jzUV+vUduuNI5pQSoAK+E7sc1c3Hn3nZVkEy4WrAQTpdoW536uMVputG7R2JhJhIu6bTQf1H3kIPUmC3eTTWCG/G9KbYbl4IsbKoP171z3YvX2TBDM2T5u9XvS8vGBWfF8WmzhnZ+hJNZaCHxEG3dnUM+2fz5IkIPhYA4blL9rhCsRMBTAbX2Xfv0QR7UMC7n0+qr93ZZ2Cv/rbaTB//Q7oG02BwsJglYXWLT+kkEx53/OGZwDq2ne4GJ9L1Tyys1BCowLuGblIdiy5Su8cyY9lbLjRqGdydEWWXlbGWogQmkgh6i7LhXeDYUMOxeX3pjWWcoyQnXbx+YCHjddMuWXBDqcqzGbabAOCD8Sdx6U14aKzJ6V6FodoxRNAtUcErhIHwdhBoRYuO+AZi5DHaLQXqOfBMBvthZgmP2h8qL+EET4d3t0dAxD1Kaln/tECsAzEAxmSPgM0/lIDxu+fP9+FRdkRRmcVtPWlV+SfBtihxFxZpgZE7BgzoPN0G4fN2bBsnnnmgq95Y/qFgZZjRIqGRgjvOMAaFjGQffvx95Vx3aMPbN56aqrWToi5chbx5LRxuNZmtZjU9DKMgaMttoRaGavWztjz+Cx+okMHN0T+HYNhNqO21gMGG8tZpgJExprrS31ABRqVzda9ASFhKIt19nKplom9kQI5bFeg8zKQURhFL0krJ3Ju72b0yrssubx/L6XywlVVg3WrzIU9tdkHg12DEF5am2586t9Tcq4FPHwZS0yehm/4UcJ5ju+kIB2uBvVxx3vNnaeLaDv9yKlrXIoTQL8mgItvSgvPz/tdivhq5MiEHKPShcDUlvFt5EIzJuu79A514wlF4BXKxzdvP0Rbj9fA2yM8cGGFBo2f243Z+8stwkwzNWX5xrv5d4wjX/yTU9lUXQkgUmmMqxjANme2rDlSHYMf6j2FAfgZARpnKqg81PL9vuLGMgAojuRzje7HDw/a2YBxLNmEPCQBMP1Cnir79l67zWqss5oqYpQK60GEIMnJhU22nL9i0YYPFnw76+fnndc9URcTiAgUxIh/g4Ph4tN4RoyuqlUqNHfCRMsJZZnr68D90xH8VqD/ZLVauV1D2A43GulRkQGuMDRRhma49wFaSuGK6GqkpUvp/Rdqqipq9V4eAQH67Owi6aN0dVVYotNZlzC264X1tSNelkVgjJ2Vdu12wIyXM1uW8BsHuoMzXIdGx3dX1eq+CMMnNU1WFz5B8g+k5pGbdU8Dz7omYolZB31MRfXHPIe6zZ3aGyxmG5h0z4QAYFRUmY0YoNDNmxurrTd2ig5OSPP386tdN3tHfsx0jx4O2ZYyo9KutrIFraW/8rXqwtPLGHB3p/6x1DAn368JhN45riwP+ZcBTkpKYru7uyOLxcK0FHtomp7VzVnszeVSDzTYNqRLp8TxsUECcqTFD7FkUthmP4VjIxFoxSxUWhkO3fv3hLTr2fDL3l06YRBXTbEJwfn1NXKHcU4Rgo+acg2rfmMoH74EI3wH7rKBYFM9BiVUv+jIlUbVGURAzwg276tqnXX2nL3p/heYLHTKvzMYlQ14SH0m+lITjg0GHnP51NafVYrUMwDaC6XP9AeepetHY8A3Br3n0ePD9xaefz9hXiMgPCpmhgcHYyyxKiwqBKBju3Elz+tVnX88Xzag9co/QwkvnvNrsQdjWxTDEHaCoDmOYs/alSsvYIBO/QLcKtkUx18gRoY6g1U4rocnmuo1HJpMatha+xD4QU2WxC4uHC+/vnD+7kN7SspdVFqoJ0vyTWDU0c3ynaMEZxgaD2jKM7J+NYADHyBEbsIE/QElFv2EANTWOt2vi4bk5GTn5OTk5ih2jFqD2U4gdKrvjyf971LFbdYFDQNnEQ/eydgLnlvvYbnnAFSZtYyxmJU6htFL/Z36PF2//JcwoKmxg6a6NfPq88OP5zcbkeijMn1Z0IvHEsU+DnD73ddWRr0JyL9LEePGjZNxSDIOEQwLM4SlpdhTvm6FdUVKCjlt5gzIPL3RUFlXJmwX3Rp1k7UFEwVwrCwdi+LDsJOnL2Eyw/JfDi+ZxFBIXlVjhYoCM+Rk5+ideP5iB0UMmdK7Z/Hd2gvSVoI9aqVlK5dip4KZ2WNWmCcBgIPjFC3OHLhwfv20BXNnhQQG7sw4c3Fyqd70uYhEE3Y8qROfSS9xv6G5Ra5oNQhnVfCmbTee2hq37w40mDiW+tKj3GnvpVuEbEn68SMfhgiFgoKTJ3Y/bdMuSKa1KSY8D5Y/z38NIJhQZixzehHEtiKfYwSCjve0lR5/CcCvEpI3f87msbt3TbLY7Q0H5g9zNzm7NkGF0TWSLQWLrxuY6CpmV3ku1ukqmpate+aVlAT8oHYh6vRbamib2M3ctfNbWYO7vdecKTiGOEqwEyGYoMk2OPH8eJtM5aZx/6Tb37k7lDVe7zdpfOnFnfsCHMcbzRYTh0DcBzV6g0Zj4L51Zg850XkQbrpzwb4z0EZ9eOOxJUsVV4MBK97qMCKjT0/ZCC4PFRm1Re1cnN1Q34HtAQBt0doUM94EMMecSADfZwAVbzr/VfNem0Uc75x4C9P2lafs+g0Kldq9Sme8fPDD8X1kyAmdKyyGEW1bgTIRg53W2ZdsOKgGhOiiSqOLzYaRyJNbRWPGdutQXZAjgjsMTCgHDGyWM1sKGJ2ggWAwQI02o6k5RWoZXD9XOwC6aC6vTxJFRVzT5eQ60IH1qTfPtwsJ62Ko0/HbXD6BxtrbQfHNk/hwBzmKDvCc22a7fqnBoLs4IG7orq49ZCfNFkPRrDl9gykW525blwEkKuEMSIEfVM/rer4W4cVzvQoYdlabFXscc/y4Ui0gaCw3qQN/D+TfpYhXCTjaIUGPEHM1IqlP1Gc7DvhVqzTktukf4AB3GXE7/xnuTLmjw07ZENdGbli9+3LvLl09h524UDPfbiVYXlFia0mBDtKO1HDLVDnv5ZcUbTpx5vSCw2ePUU0P1askbeS1AKDWZCh/Uw3j+brNMVXUrxO0Cv8eAczXZ+c5/uFtYfO+e+IiFfsu699THHLjIhF9+Db0HTKTnitREGXV9ZrTpq5SIFhTd6+N3TZv8pPPV/8Su7Rv/PyUS49WDnwrcJ6ZQMSas8UrP3slwFxXLQK4W2VWNK8oAzjSIaUW9R3HBfS3AQwAVIKrLBNjePaoQTVq49g4W6J/T9JK6cGlVwgKuq6H/J5mVb2uWKQla0iSQmjr3qpv+o0N/Kq6Vo0MBvqTVTOerHAYWKTJvh0sadXpfxvr/CaGtziGMaYQQjbXtj2XfzZizLzB1kay05HL+IevvwH2nXSzBwXcyaeeXVZWpUYb9eV+jh/kpzlPrgLG3fomedWs2L5w6O7d25uLVK/THyLw3AeAYgoN1dG/B+qbHn8tRXzcKtx6ra6OYgAzkRHi8ePbhu3t5tuT3J31AAI6ueKejd50aayQlaE4jiuqtejGnXrMdeb+7OBZtzDh7k2fZs90GOKgiPiucVoEOMuktI1EFCrBgDeADeY+b2jE56PTj875MdHfxdMo83BlAQalVqF0MthsnLHvvtf4tLxJ/u2woaifAKH0iM547rSJ8NngMXR3voF1XtxOv3LFAuE7E+Z/umbV1J8ccq/sqfxB7kPNbNfLX9Sla2f11dQrMh7wlmISf2qmzXGpqakVMdKorfI41yTH/BCB50UPb48+qVn3s0g2GfumIP5piljaLuHnYrtpilwqgnPPcvGnQ6OJQX790SV9PmjYGutgUTydb63lrb17FoaPGQdXrhw22imKZrtQNkDIuOPbnLCABHkdi0furS8wWrX1+lVsGfUEW3CFzWiP+d8OODiuxCPer41nfL/azt0jV3aRBLtNfG9SVzMNS4y1tTyj3e7u6ReYKPQNCV3+znvQmsTouk9H8Jdz4X7KI/jMqdJ2L2GkRa+j2cOH9o6QivDjiePeP7z254VTHDp6duuluXbj6q+5Lp/g/2JkjJMbnihWkZiYQ2ImQhLnWuiYa7NYlr49YFCHe7fvRjZY9K9dwbX8AC0AD506lUAIf4UxbvT29l1z/fp182sj+OHiLxdodU3f5VRWcRoayuy3axTUyWHjcamHFhp5WghWhpbrWBbvuugq1vrN6VjZpN/iFSKeWl9t/uLauaofmrmsrbyOL2G7IhI+yr5Yu4bjxM6309YvaQ0cYYs55RhhqU1jlcjbBhkBUInyQVGrl0WOJDiKptgcYseY0QZvd1/BMq0XJPq7YJbOgmZVp9j7PY17euXwW/GOc2XS8NJj+8768zhcTYfe3tI3jcSKM4/TWRgWxY7q1IMFrJkBYvm2O4qSBW96flBQkA8B8C5GyJH67SkqKsp8LcA3/vFxFotAUatOHH48sVtUnF9gKEQgD1zQiouOHdsJ/cI6QZTUDy7xHjFufrL9azZfGqFUWXkIIVxVpZ/i2cppdc7degFPQul1SguvqczAdhjrFC1d1JSl/hYAJCCHeFDCNWnbwOHqByXNCwKPHu202E6r62499HV8Fnh6L5WEtapM7Dlow2duElyt0KKNeg/shJxAwCHRNuIGPb4wmly0MNYWGOClDvCOJ2dMneW0av2SDI2hohn0lw1HFuFVLF8YOiVmoeN4yfGHVorFOqQuLa384LsF7wFA3Z2GktaaggIlRqhGGhLyUm5uieA+48dzBXzuMkBI6eXl89XvRrDDgJkj3j71xcCEGBufJ+7pE0WIPb3gp6s7ILFTBDiDAOJtgbBRd6Eur0rtLnUjQCCh4NKFalyYpaqLHeD9JC9d4UGY8PdmxHygKNH1cmolOwsI+jdlqf7Pqu4F7z16tD9mUigH2zWG9La9+3V6cPkKwXF229B/dvLM6Yo8VC30xDdZPsiksTEWI0FsEj+G7/OV0HZgl+sD+nUvDfBtxwLa1EmhzvvNKq2VS8LpLr06R63a9hOPK6Q8n+3JHMaysY4DoEXDFwx1BcCz3x2c9PaAhPYnSD5LzxZQS4LG9v9RU1CwD9N0pjQi4p9qxQ7TWwAePWeOwGIxjUKOLNXbe+U/AZycnEzU1NSQLzaeHJjYR78pvYi/LWkMakJaXOVqQl7BbXHa1QtovrwtxB9amR0X6xsVEisEmR+bLiw2sJ7e09iHze5MAIIds3tsay4btgzvaLfoqqz6rNdeeoGBIVBSUjhg3jymuqrKvnP15rKyOoVX9N1b/McCT1zOFsO+3QfRsGHjYJIpD7K5vnjgrH5E8xUgj83FAD51yifCBP+B+Rgjz0flZ0XRrm2vvjV8QOS3y79kc4Ts5hpJ6S9P2gdMjk13vI919058Uld1v/LSw2yrWhPJc5aUePZMCE50cc0HhDzvK35bxH/R/pigIFcTwsmONRWbw5uek5Ojb6EINOmdd3ozBMFHyK5qaTxxRPC6OVPqQtxkrK7RPmR3URiTyVOA3i+UyLh/ERISA6FLoQdUBPuXh2Q881vLVVy9Wv7A6ubq2f/GtSw0bGony64fr9nD/FsHrPr0U4NjR4PnytUCoG0mhWn+iwYeK0g/CwAdkqK7VAMgkSQw4B4AGqnKzWM9rlF0pmncMXjPLz88lvjAsjIzdAp0RXKpHMeXZYBbaBj2SxqUxeVwPSTS4AGEBU+rbsqYHuM1oD1FoR46Q+2ngPD5AsXjX1ePzy80XLhOBQCAG8xNYV2DY5IXLlz4ZY+h/YFhoZFdwsPrSAa6P2iob/5feXG0RPDYKVP4zQAj1OTl5fPdrxE8ceJEL4TpWQSCDMBEQ0stQlNWmjKyd9cBgc5OEBXqg6aHJMJ9bxPU1T+DPRez8fxZg1GbShdQMBpwz1dDxRD/2keQK80rr2IZDTamtslQcP1IqWjTieVa73K3Dg6ABa7cHGzDC40qy5kWQ53Cvc8Dgcq3nzlax2A8OKlV1yKMsRxbbL1b5his9rWbLj0YPP7+ef9fREGY5RWMzqZch/zbp2DbxInYVypGk/bsrLfbrS5WHa8IMPLasHJ9DiLR1l7DQraFucQ9QQDb8hoy1zlk9vTteY3L42adyz/3oeOzG092lgFgGkyqIbGennGknZ0eKnO1Hcy/7yh/vna0ADxkyhQZibCjnk15e/t++1oOTlu06PPwMaOXXLl8ETwtDeBLibBTo5bIDqfwtYc5yF2qg3qtAcb49QKPChWmTCaUHyFnssMa0JOnlbbiKiUlcuZDeGhnQ0BIgGDk6elCSAZHZ4+zwF3gWMWtMtQZPnVYLo/wcdQRGppyq2JX3D6h/GLguzLazmy06fWzgwcN+r7o7Nl/1Gr0FYDBR7Z+NRxu3RdS7tWCr9AIqdce4M+jxCheSGH/b78g9u/PeefDOSPDpWKfG5tWrD+KbUyRvt4QgxAMGjYnvnlXIlga/MBL5BNPALqfWnmteSnuGCFSrx12hCcojWoUExZ1yNNM/nK4IP3K7wHcctzT09NZyOfOwggKvLx8T/zun9yB2bP1NRYNx8fbmy7LKWQPjw5HTwQauHTzNqYJBrm4saGraxvoXWGC8hA3KFQZ8PTj+5nQWOdzijrj4EGjBkBpYeXV3JJCZuvMNcMcEXw863jEhL4T1hhqDX1fZviKBynblk+c17k2tzA8sH+/GkSSHjEj390HGHfwokROq0seSc/0GwMCkoLHTwvAbBZA2e2zzJZ4V8J3xdaHOp2OLeCKYzBNW2mbdVajrnTbibWPrrw9N/7XqyFQHDKWooixm49unvhia1i0R/B1F2/Xjr/8tE7p1z3+D1XTWigCA2EkCOZkQUFJ2ivTtPwzZxK/+/GH9MLqSmy129Cdz784U6GtG5JBKzBDmlC1ogo7B3aHYDGJQhQmeKhugsTAQLjk/IxWmxCd8bSAYrGR/fG9+nVPr1VICC6KmbV45tXOvTt+hoGZMSwi6TfbNy8D27tTp3OYYkW0mzj9ntVoGmw+dZRzomc3cg7jZI2LbMMuLa+Fe5euQLB/W9jlXgxtDpzNrVQ0MiePn/BKGj6S6di5w74d2zY6S12Ev6nauQrcz3f06dCXxWKdPJp9ZESL7sOHD0uCm3hNDBB7O84YIrZi2lFK1bgLhBfqDPr+r4rkFooY9N57chaJlmBAngSDlxSUlFx9bR58ZukSXcada4J75RVo5fDRuMigRIcfpRv1hIX/9sCOwBFLQCwmoUpZx1DViBnkGs4656PEVaoihAmi5sblYtA0GZ2fplVQiCAAscisb7d+rZj/9id9fDsHJFWklR550eiPz/488MyGfYeVhZX1drNVoq6qls/bd2xjgKf7JOXFS5wZMjHxvaIBu0b2Rg31RqgszMZhodGwwP4Mra/hFuw9f/Sz4rJbJx1yq0pUKr6ILXFyETRnF47hyndPxgi+SPRI2J1SdPb9Nh6xWgzEyczazImO4w82n13Vdvqgj9gkxQgotpVic4aysP08BjytVqfb9jq6CA4OnkdgrGIQdpdIZOsePXpkfCXAPUNCpvM4nAWBziKP7nGxu/p7B06/rqkhGBcStFYj3LifCXEJkeDp4wkMqcN0jgX1wzL41HQPV+U2QZfhHT3T7mQMK8qqWdt7bBdzbnYxeXlrulToKjAjAp9wCvQYCgiul98u7tNi9McpPz/AgKPPrj9QqCwov22z2FqPX7H+xrOHDz4Z2u8t8KuuQ53MGjzjWT3q0LYzPM2phElD2uF164+j9Z5qaJD5Q9LWPVbA6GFR2c1Oe1ffWURS6PPPv32/+Orli/zAaO84hJCmRZ8ji5g/fl4qImBFRtWTvS3fa8rrCqaPGBNQ0VivXP2PT4WamhqB1Ww69NYP3415GcDP1SLMwcHBnQhgokQS2c7XAtwnNPQQYNx/2lvdRRhj80CJG/sirSKLNJXY2dMZpGICskrKISzSF37ec9Pu5yljbYkYiIrBCIGNOvghqt7++HF1yrWj2UM4fHbJuQ27YxwcLHYTj9PWa/f7dgkYWXGr9GiLwS7h/qftRvMg76hQq0qhcuSSS5YvXbZvTN8BExcePpZhp8nW71aXI5leAxPLTcDn8gFsHNA2KHBEeAKe5ayHCi2NVqTl2CaMHsqKbOWPGqo0cYjGd7/6di732LHDmM3mzfAOddrSonNg9MC1KVkpc0U8USNtp0mjzSjDGPNLb2eqz63eyvIM8a8IadvKs/huGpTn5W/78Mzx5uLVi+NPF3swxihlwax6qUTslIh45JS0M6A1muH6k2KYN7kblsl4yEJwoFaJ6MXfryfJpSswY7M4CiborL/duOtuxhQrY/3FarNT9hqeV4mi+DIC0HDd+TOr7lU9/Y2hcXGezpqGgzaztYpks4M4YmFCxq17OLu2rslgtUqHxRyTPvmeq6919YFLNh7I2QLkLXeCC5fSwcPZCca6s7Cltgo9cm4FZXnlMHxUD32XHiGi9Ev5xz5PnjusbVDPVf9YNfMjnogdw+FwcvqE9jmLEOp3Kf8SFeUeZtVbjbrypkq5UaMvAYQzZTJ5R4GQv+/Utz/OwcDc7frhjO6/k0042AC/OOf1xZ6HDyUxu3erABhMy+XExpo8XKlRwKPSJiQWMJDYJgjiOnSAZ4U5mfX1utaLWAGIJRJgpZCLHprqNLW+bqLrt68ShJCoC4oOvLxt0bFoQMgidBe1s5lsVdVPqn1eNCise6fpGOGNVpNp5u1zV5eZbDay8tkzv4Ubtr1zvWP8yoVlCmDkvgizhGCxsEBZUYQbqmth4Vs9IJ7QoO8LbIa+fTpwhWLeN917hi8ufFp1bvP6n/s+y8wl95/bjvv07msoLirgtw3qGBvaJsD+dtzA9b0+HNB7YrvhV3ffO97LrNEXMBgyZHKnzuP7DHAb3713Qa+Fc167+emIYEf/TI8/2oD9+Nix0TGpqQftGONyL1d0w1iFtRYN8vDxBw9fL3z+6iV1TOsY0aYdR0iZswB5ecqwgOQzC6SxWkLKN39Ued0lIbYTKjcWERSXgkfX8pq+/WzxwiNHzmw+uO8QQduZBZE946znNx7HIoGoufdL4uU6Q+DktFZTU7syO7+4+mZhwQqNybzx8cGjo5e6u7lt8YmAh49ywKTVAJfrBJ4u7rg4Px+NTozAwwkd2sWKgqrqipQVq6YMcsgreFplZ7NJtPS7H9Fnn30MB38+ACfOH0Md4jrqBnbs9TWJ0Mqcwqfahxn3+SSGLjvvHW9eNrfxDb2/d8e2BFmo/0oPX9+PXxe9b0QRL7sJBh861ImprLhcVVXFrZZw0XV1HXTo0gHuPLiLI8L8EYtLQV1DCU65nAltOwWfIynUR+AkYXNyGDwkMBQl16UBT8B7snrh4bieEzo0GbQmwaaV21ibNm1Wnz2bIvWJDNoyf9qHHwzpMRgPHDGkWGk3eFRmFfGlMqm1VFsdv3rL0XCM6X1Ht++B9jIJuTwspGKyTRJga2xE6iYdYBvGdosV2XQanPzRDNTp0SVotfM85rB5oDMyYSu/Sf4UEHqfRtyAlMN7Svad30wsn7a+uteIjrnAIisqHxVNYlEI1Shq0yZ8817X8yv2rS94ljNGo1E9Of3g2qOdxw7M8PDyaHfy2yVbCCDyJm9a21xfftlw0KmjivhSipg2bRpltVq9AOwhGDOWllrEmQXzmZ7BwWjxjQs4LCzUVlBaUM139/GPiPRDFcWZODAsChlsGlynqIGA0Bh07OQFCIpwhXiuF+6h5sLHlixw8XLWFTzU1OQVZocI3aQ5QYGBwdu+37k3MDYwVV2tjpJ5u3x2ePvBBdOTFyxrPbgbicoNN/sNHZw4b+JU44CxYwVxnTsLdDoLRJUWYx+jgZme/tTq6RXE8/MLQ2wScNbDxxAVHo9ynj6AM+094dNiK0ZCCQr0DZ1z/sz22SPenhwW3sod791+EKeknrBJ+FLW5LHvft8prv0/JL7ih0sWfBtX21Sz71ruzdmX1x/Je/rggbfdbrMPen90UateHSLnDxy0LsLbZxbDYPTB1s0vpVSMMfn06SVubGw/w0sBnjRpEpdhmDiGYYwUQlJHLWJ027bRVFnJAzaNIUVR2yDhmefQGB3QWM1P2nfvHpvx6CZgEoHc3QXdvZeB+w3qj0gKm0urq7iZGbk123y70EVc7JzXxofq32U0PTCpH8vZTW6zYvrU8S2nRiFAGzwDvAYhRPgKpOJ9FdnFE1v36zSvoaJukRWRQ8Fi6UsSLGtdYfHiRfsPPhxWXORcR3H9DhqwbViXLqyrtx8hNpsHqgYj0AYD7tenM+5fcIs2YoJ1gReCbj961HT2lYVJAAARgklEQVTuyu6hH733j5skz4wHDx22NDLO/8so/9anKA5pWb907QiSxijnRhYiEIqKH9R6G8Y4vqG0kuUa7EmI5FJ4cPqs0qDWZaQ/vdfdRSxiLTl54td8+nkg34giXkT+7smT7aIzM9O1TjL6UmNd6r3yct+xwwcFy7180aE964DLZ6GQyBgoKCrERaWl4OLlKOIT1pi4BGrtul2KpI5t3d8lXfBerLElb95PDRzXDwOBGJ8Af9XXs75xRgTadOTmqYErF6/waWpUbfSJDEmkbfZERVktjuwUX52yYbfPqK8+t4slcu2z23dkp8NCbekuntT+KgUzqFcvVFvXhIpK66FPpzjQqsxgNJiBUTfg9g2FSExR+LMnDXR0WMwuiYR8JybUn6yp0dz29netvZmaGr5t/+bWXA6P7hHfZbdRbZzkIpUXH713/E6VomZKyrq9tWwulyd2EXfNTbu9X6PXBDfpVCZsszQtPnKoeQPgZcNR6k1OTmbeOIvo1br18eNjxw67z1gbK016l+KGWoiLbQUSFzd85uxRYFEssNitIHaWI5kzBzNAIw/PAGta+n02ECRWa/WwOawr2DDoBl08JuJwSatvZBDbbDbD/tWHl/A4vK+6DetVEBwdHlhVU61ycvNgV5dUivyjo/SIAT0A95oN4/Ht7Bj35/JQYGMjM5crAwuwEQsAcSkOuDq7QXZmBnZzDUDebi4gFong8vnz9OpEf7KAFuBrDQBJTjpLaHUx91Jkb7vQw9WGCChc+uNifZx/m3Yki9zPRjjhWNqxcJPVDCO7D4zefG5vhHrz5krQ68d9c+P+RIlMJAwMDTYPnTPzNw3dzwOJDx8mHwUGchISEv7pNrVXpmlRfn7708aMGXMEW1BRbRUuqakHf193DAjj5TuOsrav+8JIA8Hz9AuF7ds3Q3WdEvr0awt37jwrUal1YqmLWLBs4nuUz5NS1rqGMoh398bf374G5QWVnzbWNDXvDIQmhK/1CQuc6eLlSYRHRSIhIcD3njw2MzTNqS2upP2jY6mlNGCuqysUe3hsXf8gZ2pwQCCU5T5D9fVN4ObuDwIuF66c3Q+Bwa0YsciNkIvlzMwYT+TaVEVnWShWBK3DiC9EGh7vYOQnHzqWwzZHG8DVg6lmgoQzO7Zs7RHhHSxq1DRkrjqxOV4qEBrvT51K+Dcp2UUhYcqfM7KcpU4S7Tfbf/5Ng+C/TBGTu3S5/F337r2PWgzYSS6HJ/nZiC/gpXp4e7T38vPnKZV1zL4jpxHBYiAutk25WE75qTUaePgoD2qrVZDYPbZAIKJCV1PBJpNWw+UBQqs1TbD8ysVdHQd1xqe2nHLsecHnq5NNzu6ubIVWi87tOQZiNhd2jRwNuaVltD4qkhxdUY263LmL62qqmZGTZxJapRpJBSKwmC0gFohwbnYOxEa1qu7SMcHrk08WQGNDDXy/eD30q8iw8wrzqVuBcaBUVEJHHguXdR+I9u86oNOo1IL3J787pBEaL+hrtHM5ZvIHgZzPMun0jQJdg7yzWYsLEUkGSITVp620K5+iqPz83CPf/LJj9KsyCEdvFkLozSlizvjxWn+ZVKRnbGCx27BM7gQsFg3lNbWoTXwC3nX42A4XJ/F7Xl4u4BMUWuzr5xF8My0NKqtqLur15u41tY2cgBAveL9P39rGagUHbIzTQOBAerfEfTsP7x4vkzsxcpZT8LnLl0aERIV/08cnkDMcscl6krQ7mSysJhaJY+rqddbwcOUMRWNA5q2bTGRsAhESGomV1ZVYpzcTZQV5IJFKcWJ8J1xSUgFGnYZW1NdSocHBdMfAQIaPsJ3wCeBcObYPrYoJwgedfaGuQmUxGPXct8cMvVueV9q+Tbc43bUTl8QkgaDJoBoygYfOaNlcOqW4jJzkJoU7QWHqzDu3cz5bv6bzq/j38OHDZOAfpQiHsOspZ/YxFvPwxkYFx9PPH5avWo4S28QwVruFuHTtDg6PCNDee5gtjowKYdq2jyDy88pQaWntimtX0z9es/X7rMYmRZReawI3L6/K+/fue++J6EhUysWGhxYNVQ02qkqlsq77ag33y1WLG97V2Z3d1Fq7EFDDLjdn94eMHXz0JjR2yrT7J+/caZ12I63Wxc3H12YyIVWDAqRiOQBDQ1R4FNisNFY16VBFeTG2Wa3IzycIg80OIoEISkpyrBRJsWdEB6BwqxauggSMAgHd2pld7qzSBNhYHOZoeRPhLROgtl6yDGlxfpvPi2rswSFBrKk8RKtkzkA0NZjcgoMT0KhR+S8D+U9lEQ5BsyeMf8TjcNqwhXzc1KiA4JBgUGmaILeouFmPVCpiSIosjWkd62exaYm8/ApEkXSY2c4O9A5w3+TvHepvNFrAx9+DIElynywje1RMkwHsOi1p8/FC5Tw22PVGFENy0lgE0fHLxmqCC3h1Vp1yttFgJL39/e2rkhez1u7aCyqtmsl7nJUaHhbe3WCwoKvnTpKDho5jAvz9CA6LZUOAqLLS2jK71eRvs0N1Ynz0k2fZOcbTZw8N+OyjL/h1tQrVADeBk0/uU1AjhB2NaH5BgSlGrSGO1VDvxRaJMEvZAOlSOcrjijCfx0UDSRqLy8uQ3WSCcm/vxvAvvnB5FUUcOXKEGDVqFP3GWUT/bt1SZTJJp6amJspoNtvaxUQ/sSPs0qBSceTOcrmbhytLq1MzAj6XoNjiEb4BnlvttC3zzr2HHWi7jU+wKUYo5CG+UGRrHduG7ecdoPoq+euG8wOGn/rm3q2PBkVGVRJ2e6CT0UozEqFF6+7O9h/y9p0tB3e7bV+zMbR/0giwmCxIIpNbcjMzaYQQXyKVVdZXVJu8/INCdGoV0mm04OvjCwP6D7DfvfNAIRGLPe1WOyS2aw130u4wHA4P3b9/G+Xl5+oalLVjz54493XH2rJ5W4qb1ijUmoTSiuKGqJDQK4l+7mMKNUZbbWEO/aCk5Ja7q1tPPpfDMhj1aZ9Neuf+o1tpMwY7ycq5Cxa89LZdB0V4e3uzO3bsaHpjgDu3a3dZLpN169w2niWUSA0sLluYnZ2VrlGrQ5PGj1KxKQ598sihqR7+3jPFEskoZ2dn5v6jjIOurh7jS0qKscVuvU8g5BngHR6e9E6S53fffftUp9dzzx5N4Ujl0oakCUn1rj7ufmXPKjJlzrL2QQFBNn9ff6pOodCUV1eL3OTOdH2jkjUxaRQqKy9nCktKbQF+fhkrV61pHxERjRDJwm7OzthiY1B4UACuqCjT6XR2bsf20blXLqR92ad/t/X37z5yc3aW13/z3T9kDMbfaTT/lb2s+WHDtrSb1ydzeVzk4eFhc5HKBjaoGy81NCjAbDah0WNH244fPcqyWC0Q37o1Iijyp4+/+qp5//Avo4g9O3cWpt+5E2Q06BmKTTHtEuLL3p81N9SxrVJRUlBRWVXD7t6zGzv3WTbYGQsolVpHta6HyWw8w9BEz23bdj1yGJOUlCSJiorSldYUayiKEigbVZdPHDrRb9man5RN6iZZUEAQk52XSzI2rGoVHS1xc3GZcyv9fueuie0G5hUV3UxLuzUoPCxcJxRKajHgEJvVZqyprjEjjBx9DXjHlvXEoEEjGKPRACtX/kSTJElmZmbm6rXmyMKCAmAYBtN2W/b6zatbeuGaMdqwfKP21LmTotaRrTcuW79s1trlq2oAkEtOVhbRp28fQlFbm5P9LCeiVWQEuHm4Xx8xfnyvVwHsqEM4VlkIoddTxPONJ4sXLWoKj4iQppw+fQgDBO86cKBti4KfflhcXl5e6dO7Tx/GbDFVjhk7MSA5OZmfnJz8m0R78Xdf6wEQ9WWnboLhG9ZYJVIJ8vL2bldcWLzu4L6DnXfs2XEfGMjMLSyIVKlUfKPZzAkODN1LYNyudZs2UXaA4fXV1bsRQOrMqVPnfjBrrlEgEBSvXLY0uuUejlGjRl/AGPU6cuTgrzcfDh309kQawyJPDw+7SCgKUjYpHRQRlJKS8msD9pJvlqyUCCUzZi+YzftozoflbDbHXS5zsjCYFkolMpUrJYyotWpqCYR2z5g7e/KrwHV8/8YUMWnSuNYYg9hR7FmzZk357t27XSdNmvTS9ffoEW/PP3TsRPOdOHPmzJlNkqSjD7jd6tWrH7cY83XyolKMGeHoUWO9tv28aRJfInKiSM7avKK8JhKRP+7bs+/rFw1PXrz4oaNnMPmrr5o7b14cL7tDPilp3OwjR/avfxUIw4a8bWYArzl9+uSvDdjh4eH7EEJv5+bm8qdPnO7l5eeRyRFwDf179/0iJiFuf3OUr1n38awP57y0Xep5XW+cRbz3zjthGCF3R7Fn9erV8xBCnxIE8VJHX3Rm3rx5aatXr35prthyZahUKnTkyBHH84D+qaz3ughxHHNU/Bzny2QyrFKpHAk9eeTIEevvnfey40lJSTwAcJxLRkVF2V/WLvZH5L7Ov1culSdNGheCMXiwWLbs7duPNP0RhS1zJ0yYICBJuvkmPowJL4JAJmTD1Tv27n1pPvk6HePHjxdTFEQStGPtCDJM0Jo/a9u7774bRGJbAI3ASjAYMQTCf/I5Rc+1nDH2l/n3SoAnTx7jwzBEgM0GWfv37//NzSN/BOxmZ2iaBQQRiElsxJiu2blzf3Oz8x8Zjh+cpkkWQrSIxKSMIWjTn7QNvT9unC9DEF4MybCQHZkQQfBb2sX+iE3Pt5whIA0v8++1e3J/RNl/5r4cgf8A/DdHxn8A/g/AfzMCf7P4/0TwfwD+mxH4m8W/MoJx54QrgIyRILIBiLUAIitYhVqwiGiwigGsQgCtHMDKBdAJAHQiAJsIoJEDoBUB6NkAeg6ADvjQyOaAGURgACFoQFBvAJbUCgKOjpHYzFjE2GhXjdkKrjQjATAIACwSAIvwv4SahQAGhyCHUAGItDzQ6dlA6jnA0QFwGtngrAWg9AAiHYBYDyC0AAh1AM5aK4hoC/DA2vySgBkEYLDyQc/ig4kQiQxA6CwMHzR2MRhZXDDYKDByOKRDsB7YDgVigwUEGg6wOVno8eWXPrjpjVdyz/+YuEt7AwgpDggMCIRGsAnNmBEakUViAZvIig1cGlmlNDZwaNBLAZk4gDVCEun5AAYuG+spCunZbFBzONjA4iEj4oIZuFgPPGQEEXa4bQA+Mtt42Ir5YKUFYLNIwGrmIqtFCmASYNokQKATYDAJgTRxEGj5wNbzMFvLRmwDB3hqFuaYKCTUARY4tkkNgAQmwEIDIKHBDnwLxiKLBcksFuDSViywWRAfTCCkjZgHBsQDM+YSFhAiLeJReswmzMCidIjL1mPgGxCbYwLg6JrfA2VmUNrV3zxs6U2C/9UR/G8KMFfPw6y/CmDSjLn4Xwf4/6kI/n8LYAHFBqGD3MxgFxmBEZrAKjaBVWgHE48Gk9QORi4DBgmA0cHFPKKZKnVsChz0oKfYoGFzwcDmgwHYYAYeaIHXzISOlwn4YLTywQZ8sDACsFrEYDXzwGaVARgFwJgc5M4HB0UQZocCPlAaLrB1HOAYOMBXIeCY2SDUAggMADwDAN8IIDQ4uJgBntUOIosVpBYbcOwWENusIAA9CBkzcMAAPDACl7CCCPTApbTAJs1AkTpgcx2C9MBmmwF42v8STJkApV376yjCwS9/1cMz/4pnV7bw3V9l01/p35+iiDch8P/M+X0E/scsNMLDw5vr0nl5ecqwsICw/PzSX0ueLZ+joqLYNG3wzMsrczzE7t9i/FsBHBwczCEwHgYkrsYYBWOMniKEY8BG5wJJJjIA54uLi4tCQgLHIho0DEE4OsurAEBUVFR0w9PTky8QcEcjhHMKCkrv/zsg/G8FsL+/P5dNksMYhASO2xYYBrIIAqIJGmczJBlGEMTtgoKCkuDg4G4EQbAYhnE8OtHN8Ugwb2/vqwUFBWw+n9+WZBhDfkmJY+vp//r4twL499CIiPDzsNkodz6fX/D06dNfm50d1GA3GsMxRekdP8DvyfnvPP6/AO0m67IOGEqiAAAAAElFTkSuQmCC"
},
"dataset": [
{
"key": "__0__",
"name": "Y",
"description": "",
"type": "numeric",
"kind": "column"
},
{
"key": "__1__",
"name": "X",
"description": "",
"type": "numeric",
"kind": "column"
},
{
"key": "__2__",
"name": "Colour",
"description": "",
"type": "text",
"kind": "column"
},
{
"key": "__3__",
"name": "I",
"description": "",
"type": "text",
"kind": "column"
}
]
},
"config": {
"view": {"stroke": "transparent"},
"font": "Segoe UI",
"arc": {},
"area": {
"line": true,
"opacity": 0.6
},
"bar": {},
"line": {
"strokeWidth": 3,
"strokeCap": "round",
"strokeJoin": "round"
},
"path": {},
"point": {
"filled": true,
"size": 20
},
"rect": {},
"shape": {},
"symbol": {
"strokeWidth": 1.5,
"size": 20
},
"text": {
"font": "Segoe UI",
"fontSize": 12,
"fill": "#605E5C"
},
"axis": {
"ticks": false,
"grid": false,
"domain": false,
"labelColor": "#605E5C",
"labelFontSize": 12,
"titleFont": "wf_standard-font, helvetica, arial, sans-serif",
"titleColor": "#252423",
"titleFontSize": 16,
"titleFontWeight": "normal"
},
"axisQuantitative": {
"tickCount": 3,
"grid": true,
"gridColor": "#C8C6C4",
"gridDash": [1, 5],
"labelFlush": false
},
"axisX": {"labelPadding": 5},
"axisY": {"labelPadding": 10},
"header": {
"titleFont": "wf_standard-font, helvetica, arial, sans-serif",
"titleFontSize": 16,
"titleColor": "#252423",
"labelFont": "Segoe UI",
"labelFontSize": 13.333333333333332,
"labelColor": "#605E5C"
},
"legend": {
"titleFont": "Segoe UI",
"titleFontWeight": "bold",
"titleColor": "#605E5C",
"labelFont": "Segoe UI",
"labelFontSize": 13.333333333333332,
"labelColor": "#605E5C",
"symbolType": "circle",
"symbolSize": 75
}
},
"data": {"name": "dataset"},
"vconcat": [
{
"layer": [
{
"width": 300,
"mark": "point",
"description": "dot plot",
"encoding": {
"x": {
"field": "__1__",
"type": "quantitative",
"axis": {"title": ""}
},
"y": {
"field": "__0__",
"type": "quantitative",
"axis": {"title": ""}
},
"color": {
"field": "__2__",
"type": "nominal",
"legend": null,
"scale": null
}
}
},
{
"width": 300,
"transform": [
{
"density": "__1__",
"bandwidth": 3
}
],
"mark": {
"type": "line",
"color": "white",
"strokeWidth": 4,
"opacity": 1
},
"encoding": {
"x": {
"field": "value",
"axis": true,
"type": "quantitative"
},
"y": {
"field": "density",
"type": "quantitative",
"axis": {"labels": false}
}
}
},
{
"width": 300,
"transform": [
{
"density": "__1__",
"bandwidth": 3
}
],
"mark": {
"type": "line",
"color": "red",
"strokeWidth": 2,
"opacity": 1
},
"encoding": {
"x": {
"field": "value",
"axis": true,
"type": "quantitative"
},
"y": {
"field": "density",
"type": "quantitative",
"axis": {"labels": false}
}
}
}
],
"resolve": {
"scale": {
"y": "independent",
"color": "independent"
}
}
},
{
"width": 300,
"mark": "tick",
"description": "x-axis dash plot",
"encoding": {
"x": {
"field": "__1__",
"type": "quantitative",
"axis": {
"labels": false,
"domain": false,
"ticks": false
}
},
"color": {
"field": "__1__",
"type": "nominal",
"scale": {
"scheme": "sinebow"
},
"legend": null
}
}
}
],
"resolve": {
"scale": {
"y": "independent",
"color": "independent"
}
}
}